设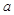
为实数，函数
，
.
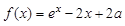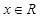（1）求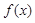
的单调区间与极值；
（2）求证：当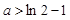
且
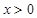时，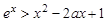
.
已知函数
．
（1）当
且
，
时，试用含
的式子表示
，并讨论
的单调区间；
（2）若
有零点，
，且对函数定义域内一切满足
的实数
有
．
①求的表达式；
②当
时，求函数
的图像与函数
的图像的交点坐标．
某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1，2，3，4，5名，“二检”中的前5名依然是这五名同学.
（1）求恰好有两名同学排名不变的概率；
（2）如果设同学排名不变的同学人数为
，求的分布列和数学期望．
（1）已知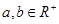
，
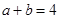，求证：
；
（2）已知
，
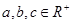，求证：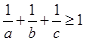
；
并类比上面的结论写出推广后的一般性结论（不需证明）.
已知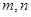
是正整数，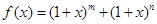
的展开式中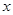
的系数为7.求
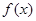展开式中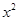
的系数的最小值，并求这时
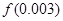的近似值（精确到0.01）．
6个人坐在一排10个座位上，则（用数字表示）.
(1)空位不相邻的坐法有多少种？
(2)４个空位只有３个相邻的坐法有多少种？
(3)４个空位至多有２个相邻的坐法有多少种？