如图,在棱长为a的正方体ABCD—A1B1C1D1中,M为A1D中点,N为AC中点.
(1)求异面直线MN和AB所成的角;
(2)求证:MN⊥AB1;
已知向量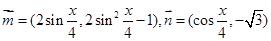 ,函数
,函数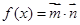 .
.
(1) 求函数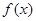 的最大值,并写出相应
的最大值,并写出相应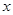 的取值集合;
的取值集合;
(2) 若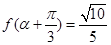 ,且
,且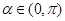 ,求
,求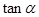 的值.
的值.
已知半径为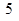 的圆的圆心在
的圆的圆心在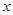 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线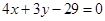 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线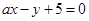
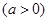 与圆相交于
与圆相交于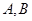 两点,求实数
两点,求实数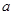 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数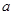 ,使得弦
,使得弦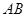 的垂直平分线
的垂直平分线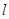 过点
过点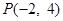 ,若存在,求出实数
,若存在,求出实数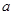 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.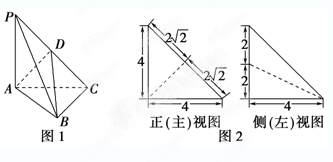
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
设直线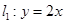 与直线
与直线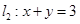 交于
交于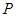 点.
点.
(1)当直线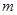 过
过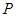 点,且与直线
点,且与直线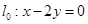 垂直时,求直线
垂直时,求直线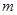 的方程;
的方程;
(2)当直线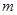 过
过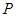 点,且坐标原点
点,且坐标原点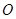 到直线
到直线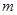 的距离为
的距离为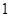 时,求直线
时,求直线 的方程.
的方程.