(本小题满分13分)设数列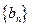 的前
的前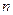 项和为
项和为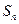 ,且
,且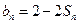 ;数列
;数列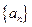 为等差数列,且
为等差数列,且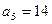 ,
,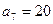 .(1)求数列
.(1)求数列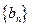 和
和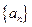 的通项公式;
的通项公式;
(2)若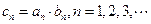 ,
,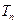 为数列
为数列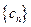 的前
的前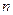 项和.求证:
项和.求证: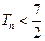 .
.
已知函数f(x)= (
(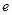 为自然对数的底数)⑴若
为自然对数的底数)⑴若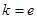 ,试确定函数
,试确定函数 的单调区间;⑵若
的单调区间;⑵若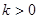 ,且对任意
,且对任意 恒
恒 成立,试确定实数
成立,试确定实数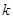 的取值范围.
的取值范围.
已知椭圆C过点A ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
(1)掷两颗骰子,其点数之和为4的概率是多少?
(2)甲、乙两人约定上午9点至12点在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,一小时之内如对方不来,则离去。如果他们二人在9点到12点之间的任何时刻到达约定地点的概率都是相等的,求他们见到面的概率。
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| 文艺节目 |
新闻节目 |
总计 |
|
| 20至40岁 |
42 |
16 |
58 |
| 大于40岁 |
18 |
24 |
42 |
| 总计 |
60 |
40 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名观众,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
(12分) 某市在每年的春节后,市政府都会发动公务员参与到植树活动 中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲:
乙: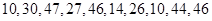
(Ⅰ)根据抽测结果,完成答题卷中的茎叶图;
(Ⅱ)根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
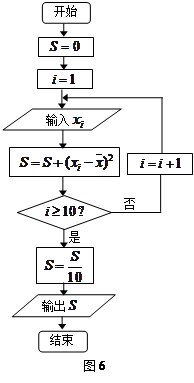
(Ⅲ)设抽测的10株甲种树苗高度平均值为 ,将这10株树苗的高度依次输入按程序框图(如图6)进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图(如图6)进行的运算,问输出的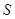 大小为多少?并说明
大小为多少?并说明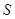 的统计学意义。
的统计学意义。