(1)掷两颗骰子,其点数之和为4的概率是多少?
(2)甲、乙两人约定上午9点至12点在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,一小时之内如对方不来,则离去。如果他们二人在9点到12点之间的任何时刻到达约定地点的概率都是相等的,求他们见到面的概率。
已知椭圆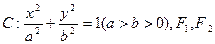 为其左、右焦点,A为右顶点,l为左准线
为其左、右焦点,A为右顶点,l为左准线 ,过
,过 的直线
的直线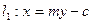 与椭圆相交于P,Q两点,且有
与椭圆相交于P,Q两点,且有
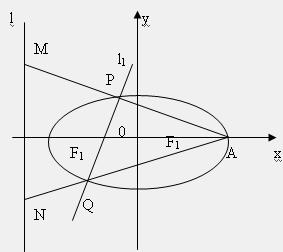
(1)求椭圆C的离心率e的最小值;
(2) ,求证:M,N两点的纵坐标之积是定值。
,求证:M,N两点的纵坐标之积是定值。
函数 在x=α处取得极小值,在x=β处取得极大值,且α2=β
在x=α处取得极小值,在x=β处取得极大值,且α2=β
(1)求α的值;
(2)求函数 在
在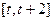 上的最大值g(t)。
上的最大值g(t)。
如图,在正三棱锥 中,底面边长是2,D是BC的中点,M在BB1上,且
中,底面边长是2,D是BC的中点,M在BB1上,且 .
.
(1)求证: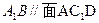 ;
;
(2)求三棱锥 的体积;
的体积;
(3)求二面角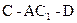 的余弦值.
的余弦值.
为了更好地服务于2010年世博会,上海某酒店随机地对最近入住的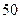 名旅客进行服务质量问卷调查,把旅客对住宿的舒适满意度与价格满意度分为五个等级:
名旅客进行服务质量问卷调查,把旅客对住宿的舒适满意度与价格满意度分为五个等级:
“1级(很不满意)”、“2级(不满意)”、“3级(一般)”、“4级(满意)”、“5级(很满意)”其结果如表所示,若在这个样本中,任选一人,其舒适度为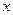 ,价格满意度
,价格满意度 .
.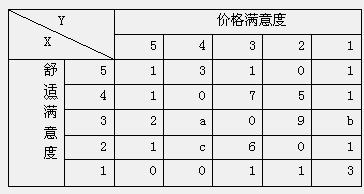
(1)根据样本中的数据求P(y=5)及P(x≥3且y=3)的值;
(2)若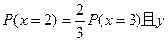 的期望值为
的期望值为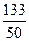 ,求a、b、c的值;
,求a、b、c的值;
(3)求该人在对价格满意(满意度不低于3)的条件下对舒适度也满意的概率.
在△ABC中,内角A、B、C的对边分别是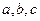 ,
,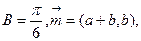
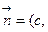
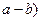 ,
,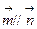 ,
,
(1)求内角A;
(2)求函数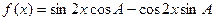 的最小正周期,并写出它的单调增区间。
的最小正周期,并写出它的单调增区间。