(本小题满分12分)已知二次函数 满足:
满足: ,
, ,且该函数的最小值为2.
,且该函数的最小值为2.
⑴ 求此二次函数 的解析式;
的解析式;
⑵ 若函数 的定义域为
的定义域为 =
=  .(其中
.(其中 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数 的值域也为
的值域也为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
本小题满分12分)一个扇形 的周长为
的周长为 ,求扇形的半径,圆心角各取何值时,此扇形的面积最大?
,求扇形的半径,圆心角各取何值时,此扇形的面积最大?
(本小题满分12分)已知函数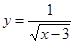 的定义域为集合A,
的定义域为集合A, 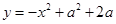 的值域为集合B.
的值域为集合B.
(1)若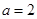 ,求
,求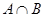 ;
;
(2) 若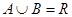 ,求实数
,求实数 的取值范围。
的取值范围。
14分)已知在数列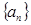 中,
中,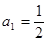 ,
,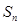 是其前
是其前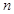 项和,且
项和,且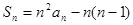 .
.
(1)证明:数列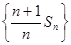 是等差数列;
是等差数列;
(2)令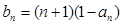 ,记数列
,记数列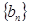 的前
的前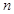 项和为
项和为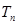 .
.
①;求证:当 时,
时,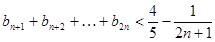
②: 求证:当 时,
时,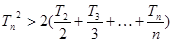
已知函数 ,
,
(1)求函数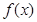 的单调区间;
的单调区间;
(2)若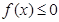 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)证明: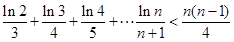 (
( 且
且 )
)