已知集合 ,
, ,
,
(1)若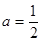 ,求
,求 ;
;
(2)若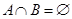 ,求实数a的取值范围.
,求实数a的取值范围.
函数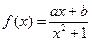 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求实数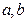 ,并确定函数
,并确定函数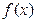 的解析式;
的解析式;
(2) 用定义证明
用定义证明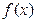 在
在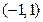 上是增函数;
上是增函数;
(3)写出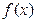 的单调减区间,并判断
的单调减区间,并判断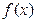 有无最大值或最小值?如有,写出最大值
有无最大值或最小值?如有,写出最大值
或最小值.(本小问不需说明理由)
、 某商品在近30天内,每件的销售价格
某商品在近30天内,每件的销售价格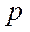 (
( 元)与时间t(天
元)与时间t(天 )的函数关系是:
)的函数关系是: ,该商品的日销售量Q(件)与时间t(天)的函数关系是
,该商品的日销售量Q(件)与时间t(天)的函数关系是
Q= -t+40 (0<t≤30,
 ),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
(I)画出函数y =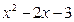 ,
,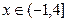 的图象;
的图象;
(II)讨论当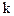 为何实数值时,方程
为何实数值时,方程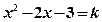 在
在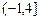 上有一个根、有两个根、没有根?
上有一个根、有两个根、没有根?
5
(I)求函数 的定义域;
的定义域;
(II)已知函数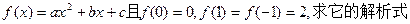 ,判断并证明该函数的奇偶性;
,判断并证明该函数的奇偶性;
、记U=R,若集合 ,
, ,则
,则
(1)求 ,
,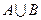 ,
, 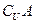 ;
;
(2)若集合 =
=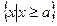 ,
,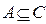 ,求
,求 的取值范围;
的取值范围;