已知直线l：mx﹣2y+2m=0（m∈R）和椭圆C：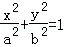
（a＞b＞0），椭圆C的离心率为
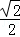，连接椭圆的四个顶点形成四边形的面积为2
．
（1）求椭圆C的方程；
（2）设直线l经过的定点为Q，过点Q作斜率为k的直线l′与椭圆C有两个不同的交点，求实数k的取值范围；
（3）设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f（m），求f（m）的表达式．
．（本小题满分12分）
鲜花扫墓渐流行，清明节期间，吉安某鲜花店某种鲜花的进货价为每束10元，销售价为每束20元，若在清明节期间内没有售
完，则在清明节营业结束后以每束5元的价格处理，据前5年的有关资料统计，这种
鲜花的需
求量X（束）服从以下分布：
| X |
20 |
30 |
40 |
50 |
| P |
0．20 |
0． 35 |
a |
0．15 |
（1）求a的值；
（2）当进货量为20，30束时，分别求出该店获利润的期望值；
（3）该店今年清明节前进该种鲜花多少束为宜？
．（本小题满分12分）
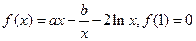已知函数
，若函数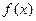
的图象在x=1处的切线平行于x轴且数列
满足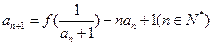
（1）求当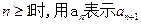
的关系式；
（2）若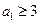
，求证：任意
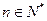，都有
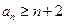成立。
（本小题满分12分）
已知函数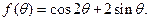
（1）求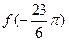
的值；
（2）若
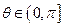且1与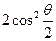
的等差中项大于1与
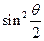的等比中项的平方，求
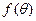的取值范围。
某化工厂生产的某种化工产品，当年产量在150吨至250吨之内，其年生产的总成本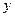
（万元）与年产量
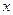（吨）之间的关系可近似地表示为
。
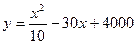（1）当年产量为多少吨时，每吨的平均成本最低，并求每吨最低平均成本
（2）若每吨平均出厂价为16万元，求年生产多少吨时，可获得最大的年利润，并求最大年利润。
如图，在直三棱柱ABC —A1B1C1 中，AB = AC = 1，AA1 =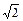 
，AB⊥AC
求异面直线BC1与AC所成角的度数