已知集合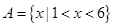 ,
,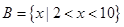 ,
,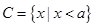 .
.
(1)求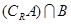 ;
;
(2)若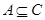 ,求
,求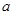 的取值范围.
的取值范围.
((本小题满分12分)
已知几何体 的三视图如图所示,其中侧视图和俯视图都是腰长为4的等腰直角三角形,正视图为直角梯形.求:
的三视图如图所示,其中侧视图和俯视图都是腰长为4的等腰直角三角形,正视图为直角梯形.求: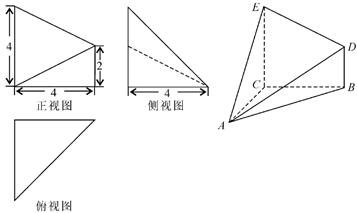
(1)异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)二面角 的正弦值;
的正弦值;
(3)此几何体的体积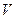 的大小.
的大小.
(本小题满分12分)
已知命题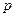 :曲线
:曲线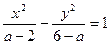 为双曲线;命题
为双曲线;命题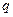 :函数
:函数 在
在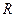 上是增函数;若命题“
上是增函数;若命题“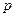 或
或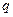 ”为真,命题“
”为真,命题“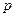 且
且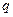 ”为假,求实数
”为假,求实数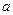 的取值范围.
的取值范围.
(本小题满分12分)
在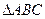 中,角
中,角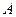 、
、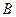 、
、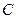 的对边分别为
的对边分别为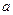 、
、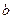 、
、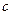 ,且满足
,且满足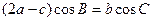 .
.
(1)求角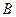 的大小;
的大小;
(2)当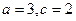 时,求
时,求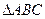 的面积.
的面积.
(本小题满分13分)已知椭圆的中心在原点,一个焦点F1(0,-2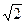 ),且离心率e满足:
),且离心率e满足: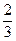 ,e,
,e,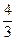 成等比数列.
成等比数列.
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-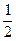
平分.若存在, 求出l的倾斜角的范围;若不存在,请说明理由.
求出l的倾斜角的范围;若不存在,请说明理由.
(本小题满分13分)已知函数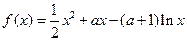 (
(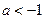 ).
).
(1)若函数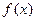 在
在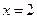 处的切线与x轴平行,求a的值,并求出函数的极值;
处的切线与x轴平行,求a的值,并求出函数的极值;
(2)已知函数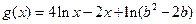 ,在(1)的条件下,若
,在(1)的条件下,若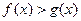 恒成立,求b的取值范围.
恒成立,求b的取值范围.