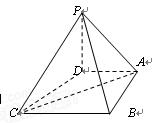
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得∠PAB=90°.点O为线段AD的中点,连接PO.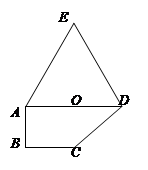
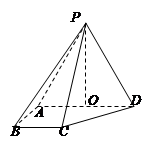
(1)求证:PO⊥平面ABCD;
(2)求异面直线CD与PA所成角的余弦值.
(本小题满分10分)
选修4-4:坐标系与参数方程选讲
已知曲线 的参数方程为
的参数方程为 (
(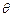 为参数),曲线
为参数),曲线 的参数方程为
的参数方程为 (
(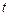 为参数).
为参数).
(1)若将曲线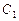 与
与 上各点的横坐标都缩短为原来的一半,分别得到曲线
上各点的横坐标都缩短为原来的一半,分别得到曲线 和
和 ,求出曲线
,求出曲线 和
和 的普通方程;
的普通方程;
(2)以坐标原点为极点,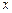 轴的非负半轴为极轴建立极坐标系,求过极点且与
轴的非负半轴为极轴建立极坐标系,求过极点且与 垂直
垂直 的直线的极坐标方程.
的直线的极坐标方程.
(本小题满分10分)
选修4-1:几何证明选讲
如图,已知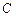 点在⊙
点在⊙ 直径的延长线上,
直径的延长线上,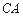 切⊙
切⊙ 于
于 点,
点, 是
是 的平分线,且交
的平分线,且交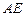 于
于 点,交
点,交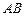 于
于 点.
点.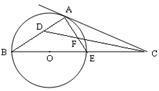
(1)求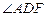 的度数;
的度数;
(2)若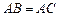 ,求
,求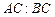 .
.
(本小题满分12分)
已知 ,
,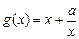
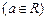 .
.
(1)求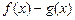 的单调区间;
的单调区间;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,证明:
时,证明: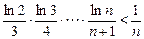 .
.
(本小题满分12分)
已知椭圆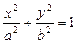 (
( )的离心率为
)的离心率为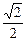 ,且短轴长为2.
,且短轴长为2.
(1)求椭圆的方程;
(2)若与两坐标轴都不垂直的直线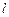 与椭圆交于
与椭圆交于 两点,
两点, 为坐标原点,且
为坐标原点,且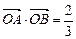 ,
,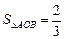 ,求直线
,求直线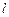 的方程.
的方程.
(本小题满分12分)
在四棱锥 中,底面
中,底面 是一直角梯形,
是一直角梯形,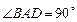 ,
, ,
,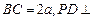 底面
底面 .
.
(1)在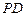 上是否存在一点
上是否存在一点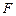 ,使得
,使得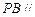 平面
平面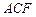 ,若存在,求出
,若存在,求出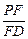 的值;
的值;
若不存在,试说明理由;
(2)在(1)的条件下,若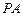 与
与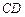 所成的角为
所成的角为 ,求二面角
,求二面角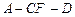 的余弦值.
的余弦值.