(本小题满分12分)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的面积.
的面积.
(本小题满分10分)某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.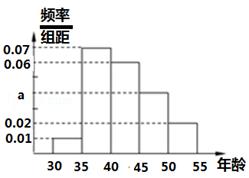
(Ⅰ)求出n,a的值;
(Ⅱ)从[45,55)岁年龄段爱好阅读的人中采用分层抽样法抽取6人,然后从这6人之中选2人为社区阅读大使,求选出的两人年龄均在[45,50)内的概率.
(本小题满分13分)已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(Ⅱ)设C、D为直线l1、l2与直线x = 4的交点,求 面积的最小值.
面积的最小值.
(本小题满分13分)设关于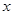 的一元二次方程
的一元二次方程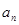
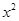

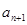
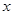
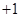
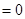 (
(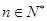 )有两根
)有两根 和
和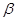 ,且满足
,且满足 .
.
(1)试用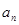 表示
表示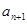 ;
;
(2)求证:数列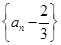 是等比数列;
是等比数列;
(3)当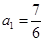 时,求数列
时,求数列 的通项公式,并求数列
的通项公式,并求数列 的前
的前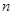 项和
项和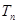 .
.
(本小题满分13分)函数y=Asin(ωx+ )(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( )>Asin(
)>Asin( )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
(本小题满分12分)在棱长为2的正方体 中,设
中,设 是棱
是棱 的中点.
的中点.
(1)求证: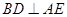 ;
;
(2)求证: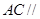 平面
平面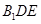 ;
;
(3)求三棱锥 的体积.
的体积.