(本小题满分12分)设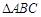 的内角
的内角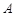 ,
,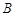 ,
, 所对的边分别为
所对的边分别为 ,
, ,
,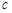 ,且
,且 .
.
(1)求角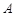 的大小;
的大小;
(2)若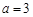 ,求
,求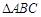 的周长
的周长 的取值范围.
的取值范围.
、(14分)某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.同时,公司每年需要付出设备的维修和工人工资等费用,第一年各种费用2万元,第二年各种费用4万元,以后每年各种费用都增加2万元.
(1)引进这种设备后,第几年后该公司开始获利;
(2)这种设备使用多少年,该公司的年平均获利最大?(参考数据: )
)
(12分)在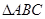 中,角
中,角 所对的边分别为
所对的边分别为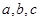 ,且满足
,且满足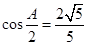 ,
, .(1)求
.(1)求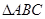 的面积;(2)若
的面积;(2)若 ,求
,求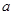 的值.
的值.
(12分)给定两个命题,p:对任意实数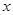 都有
都有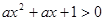 恒成立;q:关于
恒成立;q:关于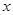 的方程
的方程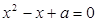 有实数根;若
有实数根;若 为真,
为真,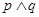 为假,求实数
为假,求实数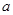 的取值范围.
的取值范围.
(本小题满分14分)已知数列{an}中,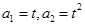 (t>0且t≠1).若
(t>0且t≠1).若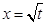 是函数
是函数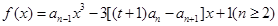 的一个极值点.
的一个极值点.
(Ⅰ)证明数列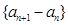 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记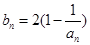 ,当t=2时,数列
,当t=2时,数列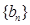 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有  。
。
(本小题满分14分)设函数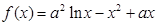 ,
, ;
;
(Ⅰ)求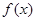 的单调递增区间;
的单调递增区间;
(Ⅱ)若 ,求使
,求使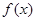 ≤
≤ 对x∈[1,e]恒成立的实
对x∈[1,e]恒成立的实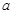 的值。
的值。
(注:e为自然对数的底数)