已知曲线C1: ,(α为参数),C2:
,(α为参数),C2: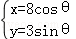 ,(θ为参数)
,(θ为参数)
(1)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为α=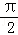 ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: ,(t为参数)距离的最小值及此时Q点坐标.
,(t为参数)距离的最小值及此时Q点坐标.
已知抛物线C: y=-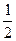 x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
已知函数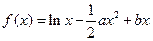 (
(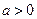 ),且
),且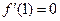 .
.
(Ⅰ)试用含有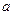 的式子表示
的式子表示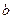 ,并求
,并求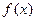 的极值;
的极值;
(Ⅱ)对于函数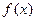 图象上的不同两点
图象上的不同两点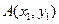 ,
,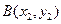 ,如果在函数图象上
,如果在函数图象上 存在点
存在点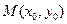 (其中
(其中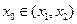 ),使得点
),使得点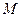 处的切线
处的切线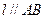 ,则称
,则称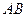 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当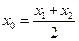 时,又称
时,又称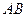 存在“中值伴随切线”. 试问:在函数
存在“中值伴随切线”. 试问:在函数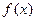 的图象上是否存在两点
的图象上是否存在两点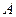 、
、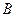 使得它存在“中值伴随切线”,若存在,求出
使得它存在“中值伴随切线”,若存在,求出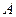 、
、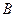 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本小题满分13分)
某鱼塘2009年初有鱼10(万条),每年年终将捕捞当年鱼总量的50%,在第二年年初又将有一部分新鱼放入鱼塘. 根据养鱼的科学技 术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼
术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼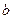 (万条).
(万条).
(I)设第 年年初该鱼塘的鱼总量为
年年初该鱼塘的鱼总量为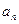 (年初已放入新鱼
(年初已放入新鱼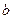 (万条),2010年为第一年),求
(万条),2010年为第一年),求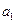 及
及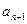 与
与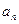 间的关系;
间的关系;
(Ⅱ)当 时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).
时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).
(本小题满分13分)
已知 ,函数
,函数 ,
,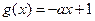 ,
, 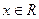 .
.
(I)求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)若在区间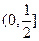 上至少存在一个实数
上至少存在一个实数 ,使
,使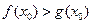 成立,试求正实数
成立,试求正实数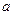 的取值范围.
的取值范围.
(本小题满分12分)
在 中,角
中,角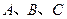 所对的边分别为
所对的边分别为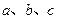 .
.
设向量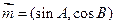 ,
,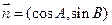
(I)若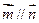 ,求角
,求角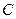 ;
;
(Ⅱ)若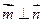 ,
, ,
,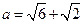 ,求边
,求边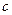 的大小.
的大小.