(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球,现从中同时取出3个球.
(1)求恰有两个黑球的概率;
(2)记取出红球的个数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点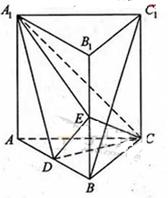
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB= ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
0.1 |
0.4 |
0.3 |
0.1 |
0.1 |
从第一个学生开始买饭时计时.
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)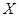 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求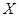 的分布列及数学期望
的分布列及数学期望
已知角 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数 ,求函数
,求函数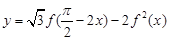 在区间
在区间 上的取值范围.
上的取值范围.
已知函数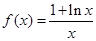 .
.
(Ⅰ)若函数在区间 其中
其中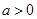 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数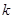 的取值范围.
的取值范围.
已知 ,数列
,数列 是首项为
是首项为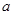 ,公比也为
,公比也为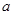 的等比数列,令
的等比数列,令
(Ⅰ)若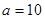 ,求数列
,求数列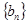 的前
的前 项和
项和 ;
;
(Ⅱ)当数列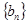 中的每一项总小于它后面的项时,求
中的每一项总小于它后面的项时,求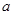 的取值范围.
的取值范围.