（本小题满分12分）对于二次函数y=x²－3x+2和一次函数y=－2x+4，把y=t（x²－3x+2）+（1－t）（－2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L.现有点A（2，0）和抛物线L上的点B（－1，n），请完成下列任务：
【尝试】
（1）当t=2时，抛物线y=t（x²－3x+2）+（1－t）（－2x+4）的顶点坐标为 ；
（2）判断点A是否在抛物线L上；
（3）求n的值；
【发现】
通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为 .
【应用】
二次函数
是二次函数y=x²－3x+2和一次函数y=－2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由
如图，已知二次函数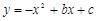
的图象经过A（
，
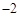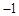），B（0,7）两点．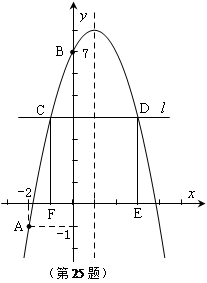
⑴求该抛物线的解析式及对称轴；
⑵当
为何值时，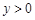
？
⑶在轴上方作平行于轴的直线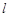
，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．
如图，Rt△ABO的顶点A是双曲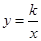线
与直线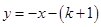
在第二象限的交点，AB⊥
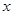轴于B且S△ABO=
.
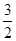（1）求这两个函数的解析式;
（2）求直线与双曲线的两个交点A，C的坐标和△AOC的面积。
某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，为了使5月份的营业额达到633.6万元，那么3月份到5月份的平均增长率为多少？
在直角坐标平面内，二次函数图象的顶点为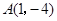
，且过点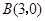
．
（1）求该二次函数的解析式；
（2）若点C（-3，12）是抛物线上的另一点，求点C关于对称轴为对称的对称点D的坐标。
某自来水公司为了鼓励市民节约用水，采取分段收费标准，若某用户居民每月应交水费y（元）是用户量x（方）的函数，其图象如图所示，根据图象回答下列问题：(10分)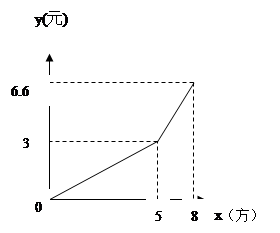 
（1）分别求出x≤5和x>5时，y与x的函数关系式；
（2）自来水公司的收费标准是什么？
（3）若某户居民交水费9元，该月
用水多少方