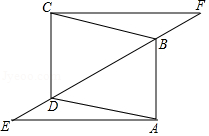
如图，已知二次函数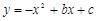的图象经过A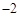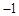（，），B（0,7）两点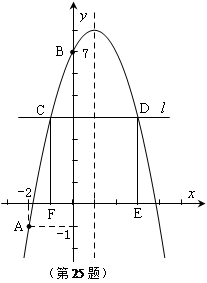．⑴求-优题课

如图，已知二次函数的图象经过A（，），B（0,7）两点．

⑴求该抛物线的解析式及对称轴；
⑵当为何值时，？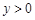
⑶在轴上方作平行于轴的直线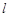，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

如图，已知 $AB$ 为 $⊙ O$ 直径， $D$ 是 $\hat{BC}$ 的中点， $DE ⊥ AC$ 交 $AC$ 的延长线于 $E$ ， $⊙ O$ 的切线交 $AD$ 的延长线于 $F$ ．

（1）求证：直线 $DE$ 与 $⊙ O$ 相切；

（2）已知 $DG ⊥ AB$ 且 $DE = 4$ ， $⊙ O$ 的半径为5，求 $\tan ∠ F$ 的值．

如图，抛物线 $y = x^{2} + bx + c$ 经过点 $A (- 1, 0)$ ， $B (0, - 2)$ ，并与 $x$ 轴交于点 $C$ ，点 $M$ 是抛物线对称轴 $l$ 上任意一点（点 $M$ ， $B$ ， $C$ 三点不在同一直线上）．

（1）求该抛物线所表示的二次函数的表达式；

（2）在抛物线上找出两点 $P_{1}$ ， $P_{2}$ ，使得△ $M P_{1} P_{2}$ 与 $ΔMCB$ 全等，并求出点 $P_{1}$ ， $P_{2}$ 的坐标；

（3）在对称轴上是否存在点 $Q$ ，使得 $∠ BQC$ 为直角，若存在，作出点 $Q$ （用尺规作图，保留作图痕迹），并求出点 $Q$ 的坐标．

如图，已知在 $Rt Δ ABC$ 中， $∠ ABC = 90 °$ ，以 $AB$ 为直径的 $⊙ O$ 与 $AC$ 交于点 $D$ ，点 $E$ 是 $BC$ 的中点，连接 $BD$ ， $DE$ ．

（1）若 $\frac{AD}{AB} = \frac{1}{3}$ ，求 $\sin C$ ；

（2）求证： $DE$ 是 $⊙ O$ 的切线．

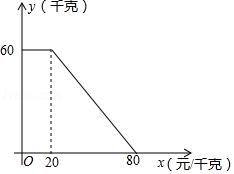
某商店以20元 $/$ 千克的单价新进一批商品，经调查发现，在一段时间内，销售量 $y$ （千克）与销售单价 $x$ （元 $/$ 千克）之间为一次函数关系，如图所示．

（1）求 $y$ 与 $x$ 的函数表达式；

（2）要使销售利润达到800元，销售单价应定为每千克多少元？

如图，已知点 $E$ ， $F$ 分别是平行四边形 $ABCD$ 对角线 $BD$ 所在直线上的两点，连接 $AE$ ， $CF$ ，请你添加一个条件，使得 $ΔABE ≅ ΔCDF$ ，并证明．