计算:(1)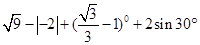 ;
;
(2)解不等式组 ,并在数轴上表示它的解集。
,并在数轴上表示它的解集。
如图,在△ABC中, ∠BAC=90°,∠ACB=30°,点A的坐标为(3,0),过B点的双曲线 ,恰好经过BC的中点D,则K的值为_______________.
,恰好经过BC的中点D,则K的值为_______________.
2008年6月1日起,某超市开始有偿提供可重复使用的三种环保购物袋,每只分别为1元、2元和3元,这三种环保购物袋每只最多分别能装大米3公斤、5公斤和8公斤。6月7日,小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20公斤散装大米,他们选购的3只环保购物袋至少应付给超市元。
使得函数值为零的自变量的值称为函数的零点。例如,对于函数 ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 的零点。己知函数
的零点。己知函数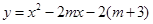 (
(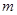 m为常数)。
m为常数)。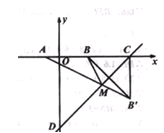
(1)当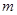 =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论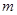 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为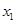 和
和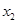 ,且
,且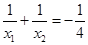 ,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线
,此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线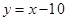 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少?