本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)已知矩阵M=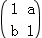 ,
,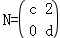 ,且
,且 ,
,
(Ⅰ)求实数a,b,c,d的值;
(Ⅱ)求直线y=3x在矩阵M所对应的线性变换下的像的方程.
(2)在直角坐标系xoy中,直线l的参数方程为 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为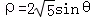 .
.
(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设圆C与直线l交于点A、B,若点P的坐标为 ,
,
求|PA|+|PB|.
(3)已知函数f(x)=|x﹣a|.
(Ⅰ)若不等式f(x)≤3的解集为{x|﹣1≤x≤5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(本小题满分16分)已知 为实数,函数
为实数,函数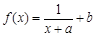 ,函数
,函数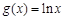 .
.
(1)当 时,令
时,令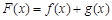 ,求函数
,求函数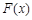 的极值;
的极值;
(2)当 时,令
时,令 ,是否存在实数
,是否存在实数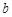 ,使得对于函数
,使得对于函数 定义域中的任意实数
定义域中的任意实数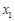 ,均存在实数
,均存在实数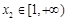 ,有
,有 成立,若存在,求出实数
成立,若存在,求出实数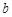 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
(本小题满分16分)已知数列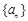 (
( ,
,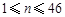 )满足
)满足 ,
, 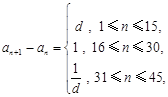 其中
其中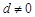 ,
, .
.
(1)当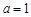 时,求
时,求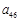 关于
关于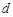 的表达式,并求
的表达式,并求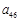 的取值范围;
的取值范围;
(2)设集合 .
.
①若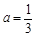 ,
,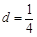 ,求证:
,求证: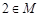 ;
;
②是否存在实数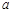 ,
,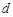 ,使
,使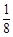 ,
,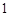 ,
,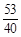 都属于
都属于 ?若存在,请求出实数
?若存在,请求出实数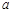 ,
,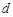 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分16分)
在平面直角坐标系 中,已知椭圆
中,已知椭圆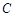 :
: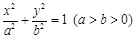 的离心率
的离心率 ,直线
,直线 过椭圆
过椭圆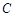 的右焦点
的右焦点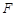 ,且交椭圆
,且交椭圆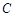 于
于 ,
, 两点.
两点.
(1)求椭圆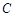 的标准方程;
的标准方程;
(2)已知点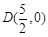 ,连结
,连结 ,过点
,过点 作垂直于
作垂直于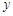 轴的直线
轴的直线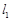 ,设直线
,设直线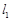 与直线
与直线 交于点
交于点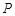 ,试探索当
,试探索当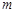 变化时,是否存在一条定直线
变化时,是否存在一条定直线 ,使得点
,使得点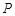 恒在直线
恒在直线 上?若存在,请求出直线
上?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为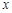 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为 (m2).
(m2).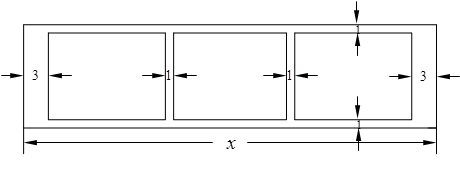
(1)求 关于
关于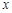 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.
(本小题满分14分)如图,四棱锥 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,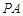 ⊥
⊥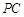 ,
,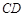 ⊥
⊥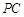 ,
, ,
,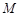 分别是
分别是 ,
,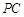 的中点,连结
的中点,连结 .求证:
.求证:
(1) ∥平面
∥平面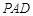 ;
;
(2) ⊥平面
⊥平面 .
.