如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.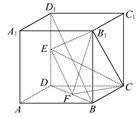
(1)求证:EF∥平面ABC1D1.
(2)求证:EF⊥B1C.
(3)求三棱锥B1-EFC的体积.
已知函数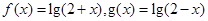 ,设函数
,设函数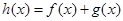 。
。
(1)求函数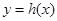 的定义域及值域;
的定义域及值域;
(2)判断函数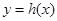 的奇偶性,并说明理由。
的奇偶性,并说明理由。
已知一次函数 满足
满足 .
.
(1)求这个函数的解析式;
(2)若函数 ,求函数
,求函数 的零点.
的零点.
已知集合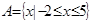 ,集合
,集合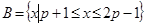
(1)当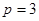 时,求集合
时,求集合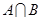 ,
,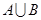 ;
;
(2)若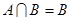 ,求实数
,求实数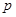 的取值范围。
的取值范围。
已知椭圆G: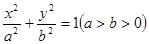 ,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.
已知直线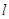 与圆C:
与圆C: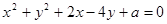 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),
(1)求实数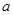 的取值范围以及直线
的取值范围以及直线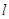 的方程;
的方程;
(2)若圆C上存在四个点到直线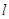 的距离为
的距离为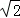 ,求实数a的取值范围;
,求实数a的取值范围;
(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使 ,求实数
,求实数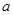 的取值范围.
的取值范围.