选修4-5:不等式选讲(本小题满分10分)已知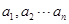 都是正数,且
都是正数,且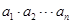 =1,求证:
=1,求证: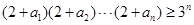
选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线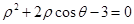 上的动点,B为直线
上的动点,B为直线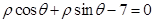 上的动点,求AB的最小值。
上的动点,求AB的最小值。
选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵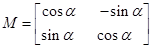 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
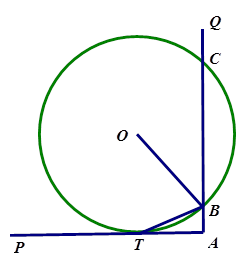
选修4-1:几何证明选讲(本小题满分10分)如图, 是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分
是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分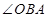
(本小题满分16分)设数列 的前n项和为
的前n项和为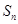 ,已知
,已知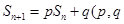 为常数,
为常数,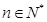 ),eg
),eg 
(1)求p,q的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在正整数m,n,使 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。