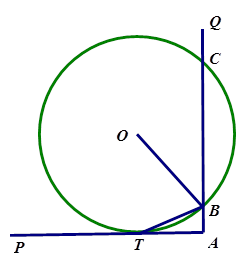
选修4-1:几何证明选讲(本小题满分10分)如图, 是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分
是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分
如图,在直四棱柱 中,底面 为等腰梯形, , , , , 、 、 分别是棱 、 、 的中点。

(Ⅰ)证明:直线
;
(Ⅱ)求二面角
的余弦值.
.
(Ⅰ)求函数
的最大值和最小正周期;
(Ⅱ)设
为
的三个内角,若
,且
为锐角,求
.



(1)求 与
与 的关系;
的关系;
(2)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求 的取值范围;
的取值范围;
(3)设 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 >
> 成立,
成立,
求实数 的取值范围.
的取值范围.


(1)求数列 的通项;
的通项;
(2)若 对任意
对任意 的整数恒成立,求实数
的整数恒成立,求实数 的取值范围;
的取值范围;
(3)设数列 ,
, 的前
的前 项和为
项和为 ,求证:
,求证:
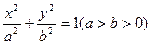
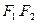
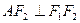
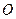
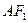
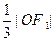
(1)求椭圆的离心率;
(2)若左焦点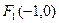 设过点
设过点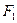 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于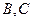 两点,线段
两点,线段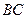 的垂直平分线与x轴交于
的垂直平分线与x轴交于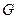 ,求点
,求点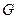 横坐标的取值范围.
横坐标的取值范围.