(本小题满分16分)设数列 的前n项和为
的前n项和为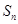 ,已知
,已知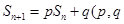 为常数,
为常数,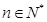 ),eg
),eg 
(1)求p,q的值;
(2)求数列 的通项公式;
的通项公式;
(3)是否存在正整数m,n,使 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
直线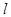 经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线
经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线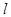 的方程。
的方程。
已知函数f(x)= ,g(x)=2|x|+a.
,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若存在x∈ R,使得f(x)≥g(x)成立,求实数a的取值范围.
坐标系与参数方程在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (t 为参数)。在极坐标系(与直角坐标系
(t 为参数)。在极坐标系(与直角坐标系 取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 。
。
(1)求圆C的直角坐标方程;
(2)设圆C与直线 交于点A,B,若点P的坐标为(2,
交于点A,B,若点P的坐标为(2, ),求|PA|+|PB|.
),求|PA|+|PB|.
如图,△ABC内接于⊙O,AB =AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB =6,BC =4,求AE.
已知函数f(x)=1n(2ax+1)+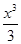 -x2-2ax(a∈R).
-x2-2ax(a∈R).
(1)若y=f(x)在[4,+∞)上为增函数,求实数a的取值范围;
(2)当a= 时,方程f(1-x)=
时,方程f(1-x)=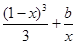 有实根,求实数b的最大值.
有实根,求实数b的最大值.