(本小题满分14分)已知函数 .
.
(1)若a>0,试判断 在定义域内的单调性;
在定义域内的单调性;
(2)若 在
在 上的最小值为
上的最小值为 ,求a的值;
,求a的值;
(3)若 在
在 上恒成立,求a的取值范围
上恒成立,求a的取值范围
选修4一5:不等式选讲
已知函数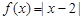 ,
,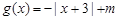 .
.
(1)解关于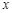 的不等式
的不等式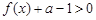 (
(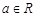 );
);
(2)若函数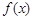 的图象恒在函数
的图象恒在函数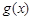 图象的上方,求
图象的上方,求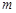 的取值范围.
的取值范围.
选修4一4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点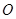 处,极轴与
处,极轴与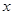 轴的正半轴重合,且长度单位相同;曲线
轴的正半轴重合,且长度单位相同;曲线 的方程是
的方程是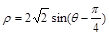 ,直线
,直线 的参数方程为
的参数方程为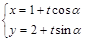 (
( 为参数,
为参数, ),设
),设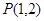 ,直线
,直线 与曲线
与曲线 交于
交于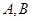 两点.
两点.
(1)当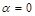 时,求
时,求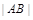 的长度;
的长度;
(2)求 的取值范围.
的取值范围.
选修4一1:几何证明选讲
如图,在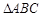 中,
中,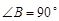 ,以
,以 为直径的圆
为直径的圆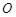 交
交 于
于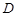 ,过点
,过点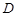 作圆
作圆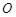 的切线交
的切线交 于
于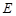 ,
,
交圆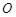 于点
于点 .
.
(1)证明: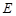 是
是 的中点;
的中点;
(2)证明: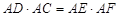 .
.
已知函数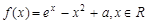 的图像在点
的图像在点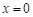 处的切线为
处的切线为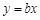 .
.
(1)求函数 的解析式;
的解析式;
(2)当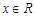 时,求证:
时,求证: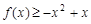 ;
;
(3)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
已知椭圆 (
( )的离心率为
)的离心率为 ,且短轴长为2.
,且短轴长为2.
(1)求椭圆的方程;
(2)若与两坐标轴都不垂直的直线 与椭圆交于
与椭圆交于 两点,
两点, 为坐标原点,且
为坐标原点,且 ,
, ,求直线
,求直线 的方程.
的方程.