（本小题满分12分） 某市有
三所高校，其学生会学习部有“干事”人数分别为
，现采用分层抽样的方法从这些“干事”中抽取
名进行“大学生学习部活动现状”调查。
（1）求应从这三所高校中分别抽取的“干事”人数；
（2）若从抽取的名干事中随机选两名干事，求选出的
名干事来自同一所高校的概率。
如图所示，
是两个垃圾中转站，
在
的正东方向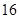
千米处，
的南面为居民生活区． 为了妥善处理生活垃圾，政府决定在的北面建一个垃圾发电厂
． 垃圾发电厂的选址拟满足以下两个要求（
可看成三个点）：①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比，比例系数相同；②垃圾发电厂应尽量远离居民区（这里参考的指标是点到直线的距离要尽可能大）． 现估测得两个中转站每天集中的生活垃圾量分别约为
吨和
吨，问垃圾发电厂该如何选址才能同时满足上述要求？
如图，已知直三棱柱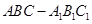
的侧面
是正方形，点
是侧面的中心，
，
是棱
的中点．
（1）求证：
平面
；
（2）求证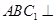：平面
平面
．
设函数
的部分图象如图所示．
（1）求函数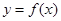
的解析式；
（2）当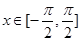
时，求
的取值范围．
已知函数
图象上点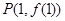
处的切线方程为
．
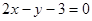（1）求函数
的单调区间；
（2）函数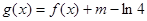
，若方程
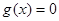在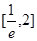
上恰有两解，求实数
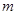的取值范围．
已知椭圆的一个顶点为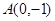
，焦点在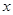
轴上，离心率为
．
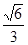（1）求椭圆的方程；
（2）设椭圆与直线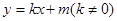
相交于不同的两点
、
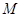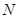，当
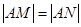时，求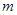
的取值范围．