某种商品原来每件售价为25元，年销售8万件．
（1）据市场调查，若价格每提高1元，销售量将相应减少2 000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？
（2）为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到x元．公司拟投入
（x2－600）万元作为技改费用，投入50万元作为固定宣传费用，投入
x万元作为浮动宣传费用．试问：当该商品明年的销售量a至少应达到多少万件时，才可能使明年的销售收入不低于原收入与总收入之和？并求出此时商品的每件定价．
某电视台的一个智力游戏节目中，有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对一个得3分，连错得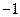
分，一名观众随意连线，他的得分记作ξ．
(1)求该观众得分ξ为非负的概率；
(2)求ξ的分布列及数学期望．
甲、乙两人破译一种密码，它们能破译的概率分别为
和
，求：
（1）恰有一人能破译的概率；（2）至多有一人破译的概率；
（3）若要破译出的概率为不小于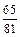
，至少需要多少甲这样的人？
甲、乙两人各射击一次，击中目标的概率分别是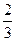
和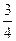
。假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响。
（Ⅰ）求甲射击4次，至少1次未击中目标的概率；
（Ⅱ）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（Ⅲ）假设两人连续两次未击中目标，则停止射击。问：乙恰好射击5次后，被中止射击的概率是多少？
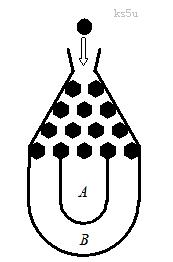
将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下落．小球在下落的过程中，将3次遇到黑色障碍物，最后落入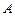
袋或
袋中．已知小球每次遇到黑色障碍物时，向左、右两边下落的概率都是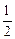
．
（Ⅰ）求小球落入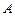袋中的概率
；
（Ⅱ）在容器入口处依次放入4个小球，记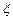
为落入袋中的小球个数，试求
的概率和的数学期望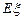
．
一个口袋中装有
个红球（
且
）和5个白球，一次摸奖从中摸两个球，两个球颜色不同则为中奖．
（Ⅰ）试用表示一次摸奖中奖的概率
；
（Ⅱ）若
，求三次摸奖（每次摸奖后放回）恰有一次中奖的概率；
（Ⅲ）记三次摸奖（每次摸奖后放回）恰有一次中奖的概率为
．当取多少时，最大？