已知函数 (
( 为常数).
为常数).
(1)若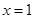 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)当 时,试判断
时,试判断 的单调性;
的单调性;
(3)若对任意的 任意的
任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数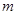 的取值范围.
的取值范围.
设集合A={a2,a+1,-1},B={2a-1,| a-2 |, 3a2+4},A∩B={-1},求实数a的值.
已知M={1,2,a2-3a-1 },N={-1,a,3},M∩N={3},求实数a的值.
设U={x∈Z|0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},
求 , (CUA)
, (CUA)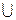 (CUB),
(CUB),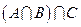 。
。
设集合 ,
,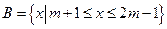 ,若
,若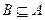 ,求实数
,求实数 的取值范围.
的取值范围.
在平面直角坐标系中,O为坐标原点,已知点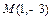 ,
, ,若点C满足
,若点C满足 ,点C的轨迹与抛物线
,点C的轨迹与抛物线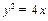 交于A、B两点.
交于A、B两点.
(I)求证: ;
;
(II)在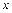 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点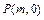 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.