已知椭圆 过点
过点 ,其焦距为
,其焦距为 .
.
(1)求椭圆 的方程;
的方程;
(2)已知椭圆具有如下性质:若椭圆的方程为 ,则椭圆在其上一点
,则椭圆在其上一点 处的切线方程为
处的切线方程为 ,试运用该性质解决以下问题:
,试运用该性质解决以下问题:
(i)如图(1),点 为
为 在第一象限中的任意一点,过
在第一象限中的任意一点,过 作
作 的切线
的切线 ,
, 分别与
分别与 轴和
轴和 轴的正半轴交于
轴的正半轴交于 两点,求
两点,求 面积的最小值;
面积的最小值;
(ii)如图(2),过椭圆 上任意一点
上任意一点 作
作 的两条切线
的两条切线 和
和 ,切点分别为
,切点分别为 .当点
.当点 在椭圆
在椭圆 上运动时,是否存在定圆恒与直线
上运动时,是否存在定圆恒与直线 相切?若存在,求出圆的方程;若不存在,请说明理由.
相切?若存在,求出圆的方程;若不存在,请说明理由.
图(1) 图(2)
(本题12分)幂函数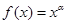 过点(2,4),求出
过点(2,4),求出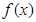 的解析式并用单调性定义证明
的解析式并用单调性定义证明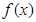 在
在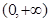 上为增函数。
上为增函数。
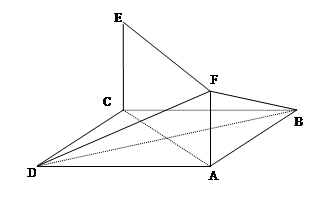
(本小题12分)如图,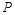 、
、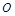 分别是正四棱柱
分别是正四棱柱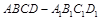 上、下底面的中
上、下底面的中
心,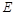 是
是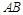 的中点,
的中点,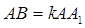 .
.
(Ⅰ)求证: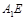 ∥平面
∥平面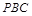 ;
;
(Ⅱ当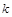 取何值时,
取何值时,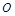 在平面
在平面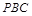 内的射影恰好为
内的射影恰好为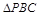 的重心?
的重心?
(本小题满分12分)
如图,在梯形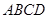 中,
中,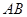 ∥
∥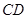 ,
,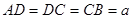 ,
,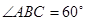 ,平面
,平面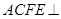 平面
平面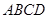 ,四边形
,四边形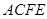 是矩形,
是矩形,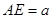 ,点
,点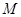 在线段
在线段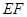 上.
上.
(1)求证:平面BCF⊥平面ACFE;
(2)当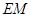 为何值时,
为何值时,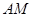 ∥平面
∥平面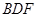 ?证明你的结论;
?证明你的结论;
(本题满分10分)
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1)求异面直线AF与BG所成的角的大小;
(2)求平面APB与平面CPD所成的锐二面角的余弦值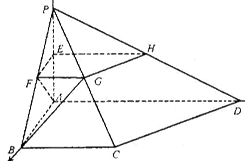
(本小题10分)如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,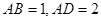 ,
,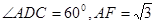
(1)求证:AC⊥BF;
(2)求点A到平面FBD的距离.