(本小题满分13分)
如图,已知点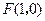 ,直线
,直线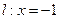 ,
, 为平面上的动点,过
为平面上的动点,过 作直线
作直线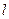 的垂线,垂足为点
的垂线,垂足为点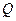 ,且
,且 求动点
求动点 的轨迹
的轨迹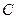 的方程;
的方程;
(本小题满分12分)
在三棱锥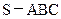 中,△ABC是边长为4的正三角形,平面
中,△ABC是边长为4的正三角形,平面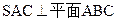 ,
,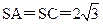 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。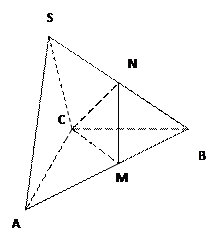
(1)证明: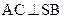 ;
;
(2)求点B到 平面CMN的距离。
平面CMN的距离。
(本小题满分12分)
如图,四棱锥 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中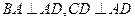 ,
,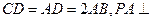 底面
底面 ,
,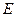 是
是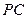 的中点.
的中点.
(1)求证: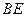 //平面
//平面 ;
;
(2)若 平面
平面 ,求异面直线
,求异面直线 与
与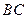 所成角的余弦值;
所成角的余弦值;
(本小题满分12分)
如图,在平行六面体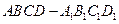 中,
中,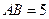 ,
, ,
,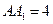 ,
, ,
, ,
,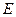 是
是
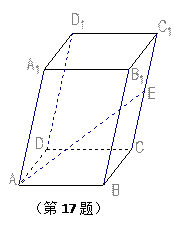
 的中点,设
的中点,设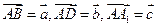 .
.
(1)用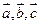 表示
表示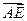
 ;
;
(2)求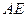 的长.
的长.
(本小题满分12分)
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有两个正根;如果
有两个正根;如果 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围.
的取值范围.