一辆轿车以12m/s的速度行驶,快到目的地时开始刹车,作匀减速直线运动,加速度大小为2m/s2,试求该车刹车后4s内以及刹车后8s内车滑行的距离。
(10分)如图所示,在水平光滑直导轨上,静止着三个质量均为m=1kg的相同小球A、B、C,现让A球以v0=2m/s的速度向着B球运动,A、B两球碰撞后粘在一起,两球继续向右运动并与C球碰撞,C球的最终速度vC=1m/s.问: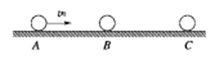
①A、B两球与C球相碰前的共同速度多大?
②两次碰撞过程中一共损失了多少动能?
图为沿x轴向右传播的简谐横波在t=1.2 s时的波形,位于坐标原点处的观察者测到在4 s内有10个完整的波经过该点。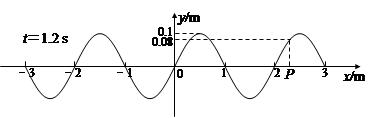
求该 ① 波的波幅、频率、周期和波速。
②画出平衡位置在x轴上P点处的质点在0-0.6 s内的振动图象。
一定质量的理想气体被活塞封闭在可导热的气缸内,活塞相对于底部的高度为h,可沿气缸无摩擦地滑动。取一小盒沙子缓慢地倒在活塞的上表面上。沙子倒完时,活塞下降了h/4。再取相同质量的一小盒沙子缓慢地倒在活塞的上表面上。外界大气的压强和温度始终保持不变,求此次沙子倒完时活塞距气缸底部的高度。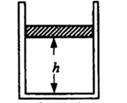
(18分)如图甲所示,直角坐标系中直线AB与横轴x夹角∠BAO=30°,AO长为a。假设在点A处有一放射源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为 、带电量为e的电子,电子重力忽略不计。在三角形ABO内有垂直纸面向里的匀强磁场,当电子从顶点A沿AB方向射入磁场时,电子恰好从O点射出。试求:
、带电量为e的电子,电子重力忽略不计。在三角形ABO内有垂直纸面向里的匀强磁场,当电子从顶点A沿AB方向射入磁场时,电子恰好从O点射出。试求: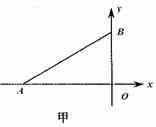
(1)从顶点A沿AB方向射入的电子在磁场中的运动时间t;
(2)速度大小为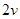 的电子从顶点A沿AB方向射入磁场(其它条件不变),求从磁场射出的位置坐标。
的电子从顶点A沿AB方向射入磁场(其它条件不变),求从磁场射出的位置坐标。
(3)磁场大小、方向保持不变,改变匀强磁场分布区域,使磁场存在于三角形ABO内的左侧,要使放射出的速度大小为 电子穿过磁场后都垂直穿过y轴后向右运动,试求匀强磁场区域分布的最小面积S。(用阴影表示最小面积)
电子穿过磁场后都垂直穿过y轴后向右运动,试求匀强磁场区域分布的最小面积S。(用阴影表示最小面积)
特警队员从悬停在空中离地235米高的直升机上沿绳下滑进行降落训练,某特警队员和他携带的武器质量共为80 kg,设特警队员用特制的手套轻握绳子时可获得200 N的摩擦阻力,紧握绳子时可获得1000 N的摩擦阻力,下滑过程中特警队员不能自由落体,至少轻握绳子才能确保安全。g取10m/s2. 求:
(1)特警队员轻握绳子降落时的加速度是多大?
(2)如果要求特警队员在空中下滑过程中先轻握绳子加速下降,再紧握绳子减速下降,且着地时的速度等于5m/s,则下落时间是多少?