如图所示,质量为m的长木块A静止于光滑水平面上,在其水平的上表面左端放一质量为m的滑块B,已知木块长为L,它与滑块之间的动摩擦因数为μ.现用水平向右的恒力F拉滑块B.
(1)当长木块A的位移为多少时,B从A的右端滑出?
(2)求上述过程中滑块与木块之间产生的内能.
已知万有引力常量G,地球半径R1,地球和太阳之间的距离r1,地球绕太阳公转的周期T1,月球半径R2,地球和月亮之间的距离r2,月球绕地球公转的周期T2,地球表面的重力加速度g。请根据已知条件用二种估算方法地球的质量M。
两颗人造卫星A、B绕地球作匀速圆周运动,运动的周期之比为TA:TB=1:27,求:①、两卫星轨道半径之比;②、两卫星运动速率之比。
如图所示,处于匀强磁场中的两根足够长。电阻不计的平行金属导轨相距1m,导轨平面与水平面成370角,下端连接阻值为R的电阻。匀强磁场方向与导轨平面垂直。质量为0.2kg。电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25。求: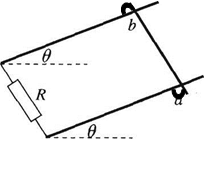
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻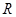 消耗的功率为
消耗的功率为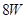 ,求该速度的大小;
,求该速度的大小;
(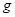 取
取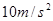 ,
,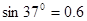 ,
,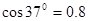 )
)
如图所示为交流发电机示意图,匝数为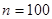 匝的矩形线圈,边长分别为
匝的矩形线圈,边长分别为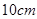 和
和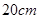 ,内阻为
,内阻为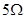 ,在磁感应强度
,在磁感应强度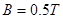 的匀强磁场中绕
的匀强磁场中绕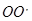 轴以
轴以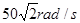 的角速度匀速转动,线圈和外部
的角速度匀速转动,线圈和外部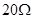 的电阻
的电阻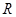 相接.求:
相接.求: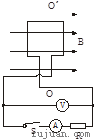
(1)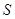 断开时,电压表示数;
断开时,电压表示数;
(2)电键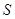 合上时,电压表和电流表示数;
合上时,电压表和电流表示数;
(3)通过电阻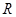 的电流最大值是多少?电阻
的电流最大值是多少?电阻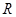 上所消耗的电功率是多少?
上所消耗的电功率是多少?
如图一台理想变压器,其原线圈 匝,副线圈
匝,副线圈 匝,并接一个
匝,并接一个 的负载电阻,其它电阻均不计。求:
的负载电阻,其它电阻均不计。求: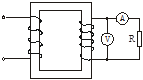
(1)当原线圈接在 直流电源上时,电压表示数为多大?
直流电源上时,电压表示数为多大?
(2)当原线圈接在输出电压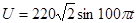
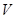 的交变电源上时,电压表示数和电流表的示数各为多大?此时变压器的输入功率为多大?
的交变电源上时,电压表示数和电流表的示数各为多大?此时变压器的输入功率为多大?