如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M。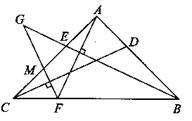
（1）求证：△ADC≌△AEB ,
（2）判断△EGM是什么三角形，并证明你的结论；
（3）猜想线段BG、AF与FG的数量关系并证明你的结论。
如图，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧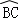
上一点，连接 BD，AD，OC，∠ADB=30°．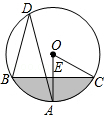
（1）求∠AOC的度数；
（2）若弦BC=6cm，求图中阴影部分的面积．
如图，在平面直角坐标系xOy中，△AOB三个顶点的坐标分别为O（0，0）、A（﹣2，3）、B（﹣4，2），将△AOB绕点O逆时针旋转90°后，点A、O、B分别落在点A'、O'、B'处．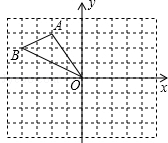
（1）在所给的直角坐标系xOy中画出旋转后的△A'O'B'；
（2）求点B旋转到点B'所经过的弧形路线的长．
如图，在正方形网格中，每个小正方形的边长都为1，△ABC的顶点都在格点（小正方形的顶点）上，将△ABC绕点A按逆时针方向旋转90°得到△AB1C1．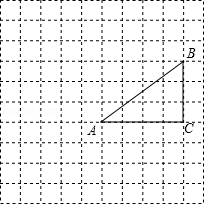
（1）在正方形网格中，画出△AB1C1；
（2）直接写出旋转过程中动点B所经过的路径长．
如图，在8×11的方格纸中，△ABC的顶点均在小正方形的顶点处．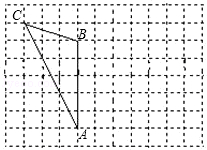
（1）画出△ABC绕点A顺时针方向旋转90°得到的△A′B′C′；
（2）求点B运动到点B′所经过的路径的长度．
如图，已知矩形ABCD的边AB=4，BC=3，按照图示位置放置在直线AP上，然后转动，当它转动一周时，求顶点A经过的路线长．