如图,已知矩形ABCD的边AB=4,BC=3,按照图示位置放置在直线AP上,然后转动,当它转动一周时,求顶点A经过的路线长.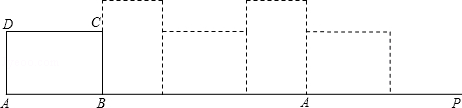
(11·台州)(12分)2011年5月19日,中国首个旅游日正式启动.某校组织了
八年级800名学生参加的旅游地理知识竞赛,李老师为了了解学生对旅游地理知识的掌握情
况,从中随机抽取了部分学生的成绩作为样本,把成绩按优秀、良好、及格和不及格4个级
别进行统计,并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).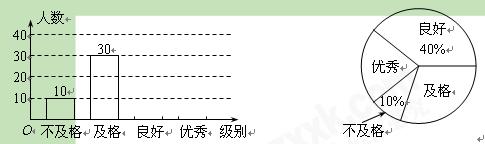
请根据以上提供的信息,解答下列问题:
(1)求被抽取部分学生的人数;
(2)请补全条形统计图,并求出扇形统计图中表示及格的扇形的圆心角度数;
(3)请估计八年级800名学生中达到良好和优秀的总人数.
(11·台州)(10分)丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你 根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位,
根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位, ≈1.7).
≈1.7).
(11·台州)(8分)毕业在即,九年级某班为纪念师生情谊,班委决定花800元
班费买两种不同单价的留念册,分别给50位同学和10位任课教师每人一本作纪念,其中送
给任课教师的留念册单价比给同学的单价多8元.请问这两种不同留念册的单价分别是多
少?
(11·台州)(8分)如图,分别延长□ABCD的边BA、DC到点E、H,使得AE
=AB,CH=CD,连接EH,分别交AD、BC于点F、G.
求证:△AEF≌△CHG.
