已知关于的一元二次方程方程有两个不相等的实数根.（1）求的取-优题课

如图，直线 $AB$ 与 $x$ 轴交于点 $A (1, 0)$ ，与 $y$ 轴交于点 $B (0, 2)$ ，将线段 $AB$ 绕点 $A$ 顺时针旋转 $90 °$ 得到线段 $AC$ ，反比例函数 $y = \frac{k}{x} (k \neq 0, x > 0)$ 的图象经过点 $C$ ．

（1）求直线 $AB$ 和反比例函数 $y = \frac{k}{x} (k \neq 0, x > 0)$ 的解析式；

（2）已知点 $P$ 是反比例函数 $y = \frac{k}{x} (k \neq 0, x > 0)$ 图象上的一个动点，求点 $P$ 到直线 $AB$ 距离最短时的坐标．

小张去文具店购买作业本，作业本有大、小两种规格，大本作业本的单价比小本作业本贵0.3元，已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同．

（1）求大本作业本与小本作业本每本各多少元？

（2）因作业需要，小张要再购买一些作业本，购买小本作业本的数量是大本作业本数量的2倍，总费用不超过15元．则大本作业本最多能购买多少本？

平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．

已知：如图，在四边形 $ABCD$ 中， $AB = CD$ ， $AD = BC$ ．

求证：四边形 $ABCD$ 是平行四边形．

证明：

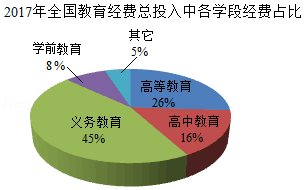
据公开报道，2017年全国教育经费总投入为42557亿元，比上年增长 $9.43 %$ ，其中投入在各学段的经费占比（即所占比例）如图，根据图中提供的信息解答下列问题．

（1）在2017年全国教育经费总投入中，义务教育段的经费总投入应该是多少亿元？

（2）2016年全国教育经费总投入约为多少亿元？（精确到 $0.1)$

已知： $∠ AOB$ ．

求作： $∠ A' O' B'$ ，使得 $∠ A' O' B' = ∠ AOB$ ．

作法：

①以 $O$ 为圆心，任意长为半径画弧，分别交 $OA$ ， $OB$ 于点 $C$ ， $D$ ；

②画一条射线 $O' A'$ ，以点 $O'$ 为圆心， $OC$ 长为半径画弧，交 $O' A'$ 于点 $C'$ ；

③以点 $C'$ 为圆心， $CD$ 长为半径画弧，与第②步中所画的弧相交于点 $D'$ ；

④过点 $D'$ 画射线 $O' B'$ ，则 $∠ A' O' B' = ∠ AOB$ ．

根据上面的作法，完成以下问题：

（1）使用直尺和圆规，作出 $∠ A' O' B'$ （请保留作图痕迹）．

（2）完成下面证明 $∠ A' O' B' = ∠ AOB$ 的过程（注 $:$ 括号里填写推理的依据）．

证明：由作法可知 $O' C' = OC$ ， $O' D' = OD$ ， $D' C' =$ 　　，

$∴$ △ $C' O' D' ≅ ΔCOD ($ 　　 $)$

$∴ ∠ A' O' B' = ∠ AOB$ ． $($ 　　 $)$