已知二次函数 .
.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)若该二次函数图象与x轴的交点为A,B,求△ABC的面积.
如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)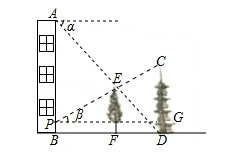
先化简: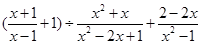 ,然后从
,然后从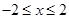 的范围内选取一个合适的整数作为x的值代入求值.
的范围内选取一个合适的整数作为x的值代入求值.
(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)
已知:如图, 是半圆
是半圆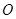 的直径,弦
的直径,弦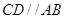 ,动点
,动点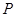 、
、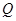 分别在线段
分别在线段 、
、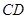 上,且
上,且 ,
, 的延长线与射线
的延长线与射线 相交于点
相交于点 、与弦
、与弦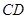 相交于点
相交于点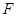 (点
(点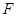 与点
与点 、
、 不重合),
不重合), ,
, .设
.设 ,
, 的面积为
的面积为 .
.

(1)求证: ;
;
(2)求 关于
关于 的函数关系式,并写出它的定义域;
的函数关系式,并写出它的定义域;
(3)当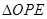 是直角三角形时,求线段
是直角三角形时,求线段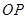 的长.
的长.
(本题满分12分,每小题满分各4分)
已知在平面直角坐标系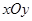 中(如图),抛物线
中(如图),抛物线 与
与 轴的负半轴相交于点
轴的负半轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,
,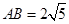 .点
.点 在抛物线上,线段
在抛物线上,线段 与
与 轴的正半轴交于点
轴的正半轴交于点 ,线段
,线段 与
与 轴相交于点
轴相交于点 .设点
.设点 的横坐标为
的横坐标为 .
.
(1)求这条抛物线的解析式;
(2)用含 的代数式表示线段
的代数式表示线段 的长;
的长;
(3)当 时,求
时,求 的正弦值.
的正弦值.
(本题满分12分,每小题满分各6分)
已知:如图,平行四边形 的对角线相交于点
的对角线相交于点 ,点
,点 在边
在边 的延长线上,且
的延长线上,且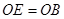 ,联结
,联结 .
.
(1)求证: ;
;
(2)如果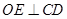 ,求证:
,求证: .
.