如果 分别是一元二次方程
分别是一元二次方程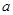
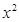 +
+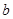
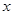 +
+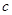 =0(
=0(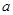 ≠0)的两根,请你解决下列问题:
≠0)的两根,请你解决下列问题:
(1)推导根与系数的关系: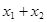 =-
=-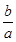 ,
, =
=
(2)已知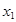 ,
,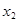 是方程
是方程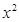 -4
-4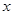 +2=0的两个实根,利用根与系数的关系求
+2=0的两个实根,利用根与系数的关系求 的值;
的值;
(3)已知sin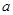 ,cos
,cos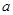 (
(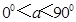 )是关于x的方程2
)是关于x的方程2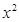 -
-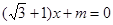 的两个根,求角
的两个根,求角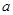 的度数.
的度数.
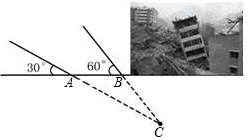
2013年10月31日20时02分在台湾花莲县,发生6.7级地震,某地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距3米,探测线与地面夹角分别是30°和 60°(如图),试确定生命所在点 C 的深度。(结果精确到0.1米,参考数据: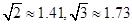 )
)
如图,在正方形网格上有△ABC和△DEF.
(1)求证:△ABC∽△DEF;
(2)计算这两个三角形的周长比;
(3)根据上面的计算结果,你有何猜想?
观察下列分母有理化的计算: ,
, ,
, ,
, …从计算结果中找出规律,并利用这一规律计算:
…从计算结果中找出规律,并利用这一规律计算:
我县今年初中的实验考试,采用学生抽签的方式决定自己的考试内容,规定:每位考生先在物理学科三个实验题(题签分别用代码B1、B2、B3表示)中抽取一个,再在化学学科三个实验题(题签分别用代码J1、J2、J3表示)中抽取一个进行实验操作考试.如果你在看不到题签的情况下,分别随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求你抽到的题签代码的下标(例如“B1”的下表为“1”)均为奇数的概率.