为了考察冰川融化的状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km 圆形考察区域，线段P1、P2是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年，冰川的边界线P1P2移动的距离为s（km），并且s与n（n为正整数）的关系是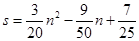
.以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别是（－4，9）、（－13，－3）.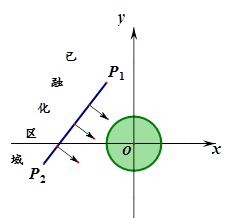
（1）求线段P1P2所在的直线对应的函数关系式；
（2）求冰川的边界线移动到考察区域所需要的最短时间.
在直角坐标系中，O为坐标原点. 已知反比例函数y=
（k>0）的图象经过点A(2，m)，过点A作AB⊥x轴于点B，且△AOB的面积为
.
（1）求k和m的值；
（2）点C（x，y）在反比例函数y=的图象上，求当1≤x≤3时函数值y的取值范围；
（3）过原点O的直线l与反比例函数y=的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值. 
已知：如图，在⊙O中M, N分别为弦AB, CD的中点，AB="CD," AB不平行于CD．
求证：∠AMN=∠CNM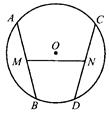
下图是一个残破的圆片示意图。请找出该残片所在圆的圆心O的位置（保留画图痕迹，不必写作法）；
如图，在平面直角坐标系中，矩形OABC的顶点A(0，3)、C(－1，0)．将矩形OABC绕原点O顺时针方向旋转90o，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线经过点C、M、N．解答下列问题：
(1)求直线BB′的 函数解析式；
(2)求抛物线的解析式；
(3)在抛物线上求出使S△PB′′ C′=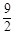
S矩形OABC的所有点P的坐标． 
扇形AOB中，OA、OB是半径，且∠AOB=90°，OA=6，点C是AB上异于A、B的动点。过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE.
（1）求证：OG=CH；
（2）当点C在AB上运动时，线段DE的长是否为定值？若为定值，请求出该值；否则，请说明理由；
（3）设CH
，CD
，求
与
之间的函数关系式.