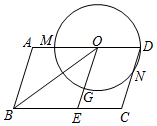
扇形AOB中,OA、OB是半径,且∠AOB=90°,OA=6,点C是AB上异于A、B的动点。过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE. (1)求证:OG=CH;
(1)求证:OG=CH;
(2)当点C在AB上运动时,线段DE的长是否为定值?若为定值,请求出该值;否则,请说明理由;
(3)设CH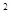
 ,CD
,CD ,求
,求 与
与 之间的函数关系式.
之间的函数关系式.
如图 ① ,直线 经过点 且平行于 y 轴,二次函数 的图象经过点 ,交直线 于点 N ,图象的顶点为 D ,它的对称轴与 x 轴交于点 C ,直线 DM 、 DN 分别与 x 轴相交于 A 、 B 两点.
( 1 )当 时,求点 N 的坐标及 的值;
( 2 )随着 a 的变化, 的值是否发生变化?请说明理由;
( 3 )如图 ② , E 是 x 轴上位于点 B 右侧的点, , DE 交抛物线于点 F .若 ,求此时的二次函数表达式.

(算一算)
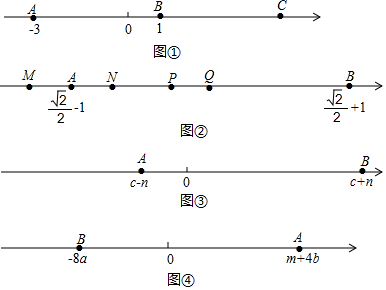
如图 ① ,点 A 、 B 、 C 在数轴上, B 为 AC 的中点,点 A 表示 ,点 B 表示 1 ,则点 C 表示的数为 , AC 长等于 ;
(找一找)
如图②,点 M 、 N 、 P 、 Q 中的一点是数轴的原点,点 A 、 B 分别表示实数 、 , Q 是 AB 的中点,则点 是这个数轴的原点;
(画一画)
如图 ③ ,点 A 、 B 分别表示实数 、 ,在这个数轴上作出表示实数 n 的点 E (要求:尺规作图,不写作法,保留作图痕迹);
(用一用)
学校设置了若干个测温通道,学生进校都应测量体温,已知每个测温通道每分钟可检测 a 个学生.凌老师提出了这样的问题:假设现在校门口有 m 个学生,每分钟又有 b 个学生到达校门口.如果开放 3 个通道,那么用 4 分钟可使校门口的学生全部进校;如果开放 4 个通道,那么用 2 分钟可使校门口的学生全部进校.在这些条件下, a 、 m 、 b 会有怎样的数量关系呢?
爱思考的小华想到了数轴,如图 ④ ,他将 4 分钟内需要进校的人数 记作 ,用点 A 表示;将 2 分钟内由 4 个开放通道检测后进校的人数,即校门口减少的人数 记作 ,用点 B 表示.
① 用圆规在小华画的数轴上分别画出表示 、 的点 F 、 G ,并写出 的实际意义;
② 写出 a 、 m 的数量关系: .
如图, 中, 的平分线 交边 于点 , ,以点 为圆心, 长为半径作 ,分别交边 、 于点 、 .点 在边 上, 交 于点 , 为 的中点.
( 1 )求证:四边形 为菱形;
( 2 )已知 ,连接 ,当 与 相切时,求 的长.
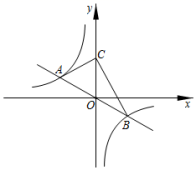
如图,正比例函数 的图象与反比例函数 的图象交于点 和点 .
( 1 ) , ;
( 2 )点 在 轴正半轴上. ,求点 的坐标;
( 3 )点 在 x 轴上, 为锐角,直接写出 的取值范围.
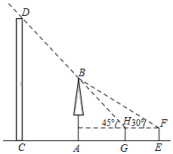
如图,点 E 与树 AB 的根部点 A 、建筑物 CD 的底部点 C 在一条直线上, .小明站在点 E 处观测树顶 B 的仰角为 ,他从点 E 出发沿 EC 方向前进 到点 G 时,观测树顶 B 的仰角为 ,此时恰好看不到建筑物 CD 的顶部 D ( H 、 B 、 D 三点在一条直线上).已知小明的眼睛离地面 ,求建筑物 CD 的高度(结果精确到 ).(参考数据: , .)