为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
| 运动鞋价格 |
甲 |
乙 |
| 进价(元/双) |
m |
m﹣20 |
| 售价(元/双) |
240 |
160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
(1) 计算:(3-π)0+|―2013|-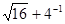
(2) 已知3a2+a=2,求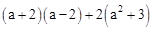 +a的值.
+a的值.
已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.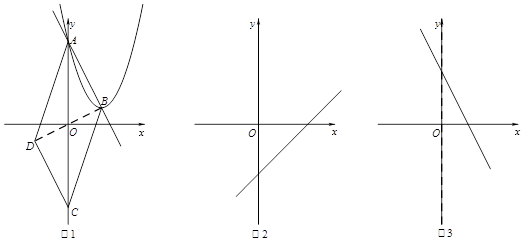
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的表达式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的表达式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.用含b的代数式表示m、n的值.
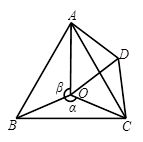
如图,点 是等边
是等边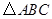 内一点,
内一点,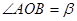 ,
, 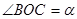 .将
.将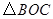 绕点
绕点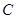 按顺时针方向旋转
按顺时针方向旋转 得
得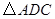 ,连接
,连接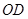 .
.
(1)当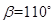 ,
,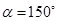 时,试判断
时,试判断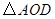 的形状,并说明理由.
的形状,并说明理由.
(2)请写出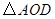 是等边三角形时
是等边三角形时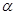 、
、 的度数.
的度数.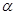 = 度;
= 度;  =度.
=度.
(3)探究:若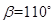 ,则
,则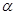 为多少度时,
为多少度时,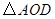 是等腰三角形?
是等腰三角形?
(只要写出探究结果)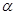 = ;
= ;
已知关于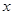 的一元二次方程
的一元二次方程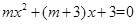 .
.
(1)求证:方程有两个实数根;
(2)当此方程有一个根是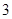 时,求关于
时,求关于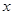 的二次函数
的二次函数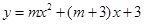 的表达式;
的表达式;
(3)在(2)的条件下,若点A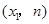 与点B
与点B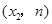 (
(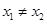 )在关于
)在关于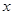 的二次函数
的二次函数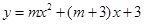 的图象上,将此二次函数的图象在
的图象上,将此二次函数的图象在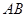 上方的部分沿
上方的部分沿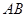 翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 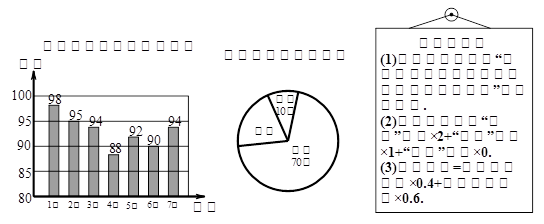
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?