(本题10分)集合 ,
, ,求
,求 ,
, ,
, .
.
(本小题满分12分)已知集合 ,
, .
.
(1)当 时,求集合
时,求集合 ,
, ;
;
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.
(本小题满分12分) 已知全集 ,若
,若 ,
, ,求实数
,求实数 的值.
的值.
(本小题满分12分)设函数 定义在R上,对于任意实数
定义在R上,对于任意实数 ,恒有
,恒有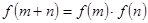 ,且当
,且当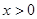 时,
时,
(1)求证: 且当
且当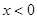 时,
时,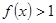
(2)求证: 在R上是减函数;
在R上是减函数;
(3)设集合 ,
,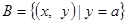 ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。
(本小题满分12分)设关于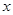 的方程
的方程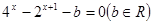 ,
,
(1)若方程有实数解,求实数 的取值范围;
的取值范围;
(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。
(本小题满分12分)某商品在近30天内每件的销售价格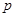 (元)与时间
(元)与时间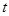 (天)的函数关系是
(天)的函数关系是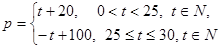 。该商品的日销售量Q(件)与时间
。该商品的日销售量Q(件)与时间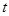 (天)的函数关系是
(天)的函数关系是 ,求这种商品的日销售额的最大值,并指出日销售金额最大的一天是30天中的第几天?
,求这种商品的日销售额的最大值,并指出日销售金额最大的一天是30天中的第几天?