(本小题满分13分)三棱锥P-DEF中, 顶点P在平面DEF上的射影为O.
(Ⅰ)如果PE=PF=PD, 证明O是三角形DEF的外心(外接圆的圆心)
(Ⅱ)如果 ,
,  ,
,  ,
,  ,证明: O是三角形DEF的垂心(三条高的交点)
,证明: O是三角形DEF的垂心(三条高的交点)
如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC, AB∥DC.
(1)求证:D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
已知A={x|x2-3x+2≤0},B={x|x2-(a+1)x+a≤0}.
(1)若A⊆B,求a的取值范围;
(2)若B⊆A,求a的取值范围.
(本小题满分12分)如图所示,在多面体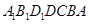 ,四边形
,四边形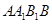 ,
,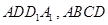 均为正方形,
均为正方形,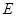 为
为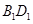 的中点,过
的中点,过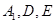 的平面交
的平面交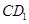 于
于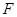

(1)证明: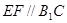 ;
;
(2)(理科做) 求二面角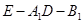 余弦值.
余弦值.
(3)(文科做) 若正方形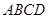 边长为2,求多面体
边长为2,求多面体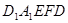 的体积.
的体积.
(本小题满分12分)如图,在正四棱台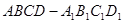 中,
中,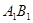 =1,
=1,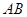 =2,
=2,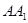 =
=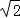 ,
,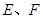 分别是
分别是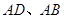 的中点.
的中点.
(1)求证:平面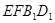 ∥平面
∥平面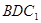 ;
;
(2)求证:平面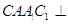 平面
平面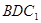 ;
;
(3)(文科不做)求直线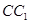 与平面
与平面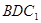 所成的角.
所成的角.
(本小题满分10分)如图,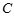 、
、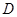 是以
是以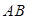 为直径的圆上两点,
为直径的圆上两点, ,
,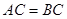 ,
,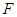 是
是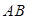 上一点,且
上一点,且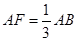 ,将圆沿直径
,将圆沿直径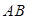 折起,使点
折起,使点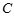 在平面
在平面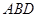 的射影
的射影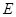 在
在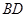 上,已知
上,已知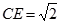 .
.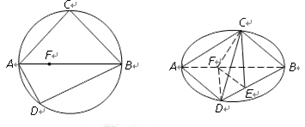
(1)求证: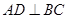 ;
;
(2)求三棱锥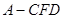 的体积.
的体积.