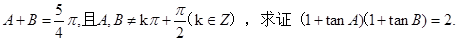(本小题满分12分)设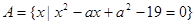 ,
,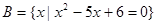 ,
,
(Ⅰ)若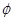

 ,且
,且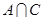 =
=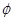 ,求实数
,求实数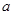 的值;
的值;
(Ⅱ) =
=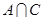
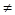
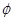 ,求
,求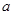 的值.
的值.
如图,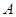 是以
是以 为直径的
为直径的 上一点,
上一点, 于点
于点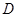 ,过点
,过点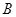 作
作 的切线,与
的切线,与 的延长线相交于点
的延长线相交于点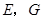 是
是 的中点,连结
的中点,连结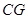 并延长与
并延长与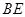 相交于点
相交于点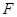 ,延长
,延长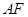 与
与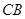 的延长线相交于点
的延长线相交于点 .
.
(1)求证: ;
;
(2)求证: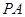 是
是 的切线;
的切线;
(3)若 ,且
,且 的半径长为
的半径长为 ,求
,求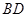 和
和 的长度.
的长度.
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
(本题可以参考两个分类变量x和y有关系的可信度表:)
甲乙两人同时同地沿同一路线走到同一地点,甲有一半时间以速度m行走,另一半时间以速度n行走;有一半路程乙以速度m行走,另一半路程以速度n行走,如果m ¹ n,问:甲乙两人谁先到达指定地点?
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
已知