如图所示的正方形网格中,△ 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: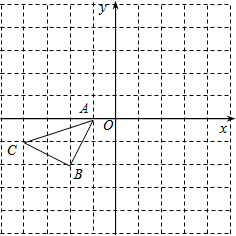
(1)以 点为旋转中心,将△
点为旋转中心,将△ 绕点
绕点 顺时针旋转
顺时针旋转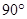 得△
得△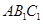 ,画出△
,画出△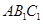 。
。
(2)画出△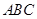 关于坐标原点
关于坐标原点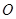 成中心对称的△
成中心对称的△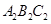 ,并写出点A2、B2、C2各点坐标。
,并写出点A2、B2、C2各点坐标。
如图,在下列矩形ABCD中,已知:AB=a,BC=b(a<b),假定顶点在矩形边上的菱形叫做矩形的内接菱形,现给出(Ⅰ)、(Ⅱ)、(Ⅲ)三个命题: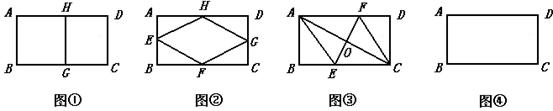
命题(Ⅰ):图①中,若AH=BG=AB,则四边形ABGH是矩形ABCD的内接菱形;
命题(Ⅱ):图②中,若点E、F、G和H分别是AB、BC、CD和DE的中点,则四边形EFGH是矩形ABCD的内接菱形;
命题(Ⅲ):图③中,若EF垂直平分对角线AC,变BC于点E,交AD于点F,交AC于点O,则四边形AECF是矩形ABCD的内接菱形.
请解决下列问题:命题(Ⅰ)、(Ⅱ)、(Ⅲ)都是真命题吗?请你在其中选择一个,并证明它是真命题或假命题;
画出一个新的矩形内接菱形(即与你在(1)中所确认的,但不全等的内接菱形).
试探究比较图①,②,③中的四边形ABGH、EFGH、AECF的面积大小关系
如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
求抛物线的解析式;
设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时的点E的坐标.
如图,在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心、OB长为半径的圆交BC于点D,DE⊥AC交AC于点E.
求证:DE是⊙O的切线;
若⊙O与AC相切于点F,AB=AC=5,sinA=
 ,求⊙O半径的长度.
,求⊙O半径的长度.
如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2km,点B位于点A北偏东60°方向且与A相距10km处,现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
求观测点B到航线l的距离;
求该轮船航行的速度.(结果精确到0.1km/h)(参考数据,
 =1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)
=1.73,sin76°=0.97,cos76°=0.4,tan76°=4.01)
张老师为了了解学生训练前后定点投篮情况(规则为在罚球线投篮10次,统计进球个数),对本班男、女生的投中个数进行了统计,并绘制成如下频数分布折线图.请根据图①,回答下列问题:
①求全班的总人数;
②求男生投中个数的中位数;通过张老师对投篮要点的讲解和示范,一周后学生的投中个数比训练前明显增加,全班投中个数变化的人数的扇形统计图如图②所示,求训练后投篮个数增加3次的学生人数和全班增加的投篮总个数.
