四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF-BF=EF;
(2)如图2,在(1)条件下,AG= BG,求
BG,求 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE= 。(直接写出结果)
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下: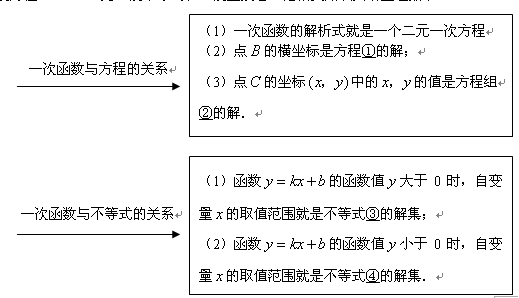
(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
①;②;③;④;
(2)如果点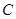 的坐标为
的坐标为 ,那么不等式
,那么不等式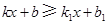 的解集是.
的解集是.
如图,一次函数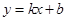 的图象与反比例函数
的图象与反比例函数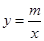 的图象交于
的图象交于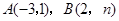 两点,直线
两点,直线 分别交
分别交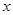 轴、
轴、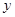 轴于
轴于 两点.
两点.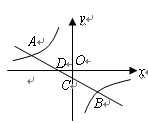
(1)求上述反比例函数和一次函数的解析式;
(2)求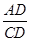 的值.
的值.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.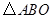 的三个顶点
的三个顶点 都在格点上.
都在格点上.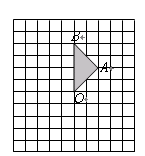
(1)画出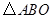 绕点
绕点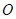 逆时针旋转
逆时针旋转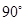 后得到的三角形;
后得到的三角形;
(2)求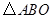 在上述旋转过程中所扫过的面积.
在上述旋转过程中所扫过的面积.
(1)计算: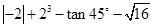 (2)解方程:
(2)解方程: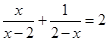
如图,四边形 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点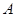 在
在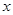 轴上,点
轴上,点 在
在 轴上,将边
轴上,将边 折叠,使点
折叠,使点 落在边
落在边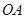 的点
的点 处.已知折叠
处.已知折叠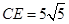 ,且
,且 .
.
(1)判断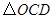 与
与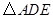 是否相似?请说明理由;
是否相似?请说明理由;
(2)求直线 与
与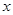 轴交点
轴交点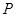 的坐标;
的坐标;
(3)是否存在过点 的直线
的直线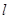 ,使直线
,使直线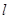 、直线
、直线 与
与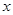 轴所围成的三角形和直线
轴所围成的三角形和直线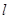 、直线
、直线 与
与 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.