在Rt△ABC中，∠CAB=90°，AB=AC．
（1）如图①，过点A在△ABC外作直线MN，BM⊥MN于M，CN⊥MN于N．①判断线段MN、BM、CN之间有何数量关系，并证明；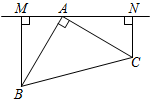
②若AM=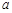
，BM=
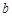，AB=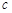
，试利用图①验证勾股定理
=
；
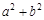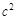（2）如图②，过点A在△ABC内作直线MN，BM⊥MN于M，CN⊥MN于N，判断线段MN、BM、CN之间有何数量关系？（直接写出答案）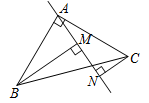
解分式方程：
﹣
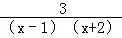=1．
先化简再求值（
+
）÷
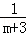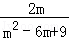，其中m=
．
如图，△ABC中，AB=AC=5，BC=8．
（1）求△ABC的面积；
（2）若过点C作AB平行线CD，并使CD=BC，连结BD，交AC于点E．
①那么∠ACB与∠D有怎样的数量关系？证明你的结论；
②那么△ABE与△BCE的面积比是多少？写出求解过程．
如图，已知∠ABC=90°，点P为射线BC上任意一点（点P与点B不重合），分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ，连接QE并延长交BP于点F．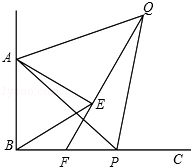
（1）试说明：∠AEQ=90°；
（2）猜想EF与图中哪条线段相等（不能添加辅助线产生新的线段），并说明理由．
如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．
求证：（1）∠ECD=∠EDC；
（2）OC=OD；
（3）OE是线段CD的垂直平分线．