如图：在数轴上A点表示数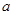
，B点示数
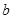，C点表示数c,b是最小的正整数，
且a、b满足|a+2|+ （c－7）2=0．
（1）a= ，b= ，c= ；
（2）若将数轴折叠，使得A点与C点重合，则点B与数 表示的点重合；
（3）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．
则AB= ，AC= ，BC= ．（用含t的代数式表示）
（4）请问：3BC－2AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
如图，一次函数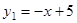
与反比例函数
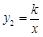的图象交于A（1，m）、B（4，n）两点．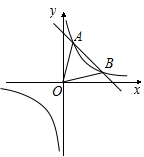
（1）求A、B两点的坐标和反比例函数的解析式；
（2）根据图象，直接写出当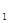y
＞y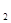
时x的取值范围；
（3）求△AOB的面积．
如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处，折痕交OA于点C，求整个阴影部分的周长和面积。
在如图所示的网格图中．每个小正方形的边长均为1个单位，又在Rt△
中，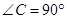
，
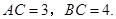
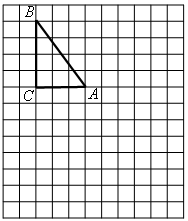
（1）试在图中作出△以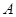
为旋转中心，沿顺时针方向旋转90°后的图形△
；
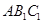（2）若点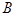
的坐标为（－3，5），试在图中画出直角坐标系，并写出
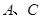的坐标；
（3）在上述坐标系中作出△关于原点对称的图形△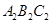
，写出
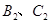的坐标．
【原创题】（1）计算：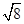
－（
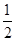）-1－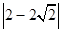
（2）先化简，再求值：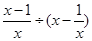
。其中x=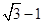
已知如图，
是△
的边
上一点，
∥
，交边
于点
，延长至点
，使
，联结
，交边于点
，联结
（1）求证：
；
（2）如果
，求证：