（本题14分）[来源二次函数的图像的顶点为A（2，-4），且经过点B（5，5）
（1）求抛物线解析式，并画出二次函数图象草图.
（2）若点E1（n2+2，y1）、E2（-n2-1，y2）、E3（n4+3，y3）在抛物线上，且0<n<1，试比较y1、y2、y3的大小.
（3）二次函数的图像与X轴交于C、D两点，点G在抛物线上，点H在抛物线对称轴上，若以C、D、G、H为顶点的四边形是平行四边形，求点G的坐标.
阅读下题的计算方法。
计算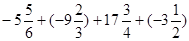
。
解：原式=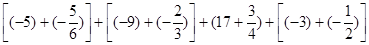
= 
=
=
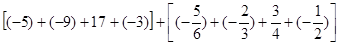
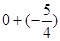
上面这种解题方法叫做拆项法，按此方法计算：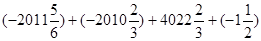
洋洋有4张卡片写着不同的数字的卡片，请你按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字乘积最大，如何抽取？最大值是多少？(2分)
（2）从中取出2张卡片，使这2张卡片上数字组成一个最大的数，如何抽取？最大的数是多少？
（3）将这4张卡片上的数字用学过的运算方法，使结果为24．写出运算式子（一种即可）．
定义新运算：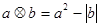
，如
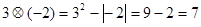，计算下列各式。
（1）
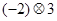（2）
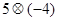（3）
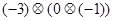
已知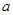
、
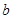互为相反数，
、
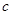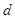互为倒数，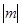
=2，求代数式
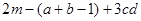的值。
某天早上，一辆交通巡逻车从A地出发，在东西向的马路上巡视，中午到达B地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下。（单位：km）
（1）B地在A地哪个方向，与A地相距多少千米？
（2）巡逻车在巡逻过程中，离开A地最远是多少千米？
（3）若每km耗油0.3升，问共耗油多少升？