如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:
…
(1)在第n个图中,每一横行共有________块瓷砖,每一竖列共有________块瓷砖;(均用含n的代数式表示)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与n的函数关系式;(不要求写出自变量n的取值范围)
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
(4)若黑色瓷砖每块4元,白色瓷砖每块3元,则购买506块瓷砖共需花费多少元?
(5)是否存在黑色瓷砖与白色瓷砖的块数相等的情形?请通过计算说明理由.
(本题满分10分)如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC∶CA=4∶3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S.
(本题满分10分)某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件
(1)假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x间的函数关系式,并注明x的取值范围.
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
吸烟有害健康!你知道吗,即使被动吸烟也大大危害健康.有消息称,我国准备从2011年元月一日起在公众场所实行“禁烟”,为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下统计图:
根据统计图解答:
(1)同学们一共随机调查了多少人?
(2)请你把统计图补充完整;
(3)如果在该社区随机咨询一位市民,那么该市民支持“强制戒烟”的概率是多少?假定该社区有1万人,请估计该地区大约有多少人支持“警示戒烟”这种方式.
试确定实数a的取值范围,使不等式组 恰有两个整数解.
恰有两个整数解.
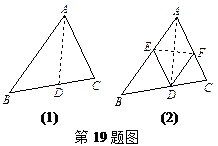
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.