(本题10分)如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.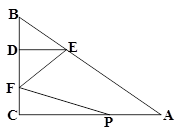
(1)线段AC的长= ;
(2)当△PCF与△EDF相似时,求t的值;
(3)连接PE,以PE所在直线为对称轴作线段DC的轴对称图形D′C′,若点D′恰好落在线段AE上,求t的值。
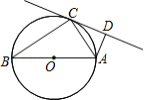
如图, 是
是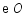 的直径,
的直径,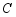 是
是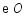 上一点,
上一点,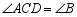 ,
,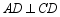 .
.
(1)求证: 是
是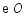 的切线;
的切线;
(2)若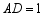 ,
,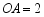 ,求
,求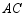 的值.
的值.
解不等式组: ,并把解集在数轴上表示出来.
已知,抛物线 经过原点,顶点为
经过原点,顶点为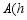 ,
,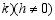 .
.
(1)当 ,
, 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)若抛物线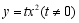 也经过
也经过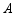 点,求
点,求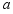 与
与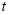 之间的关系式;
之间的关系式;
(3)当点 在抛物线
在抛物线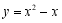 上,且
上,且 时,求
时,求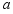 的取值范围.
的取值范围.
福州市 年常住人口数统计如图所示.
年常住人口数统计如图所示.
根据图中提供的信息,回答下列问题:
(1)福州市常住人口数,2015年比2014年增加了 万人;
(2)与上一年相比,福州市常住人口数增加最多的年份是 ;
(3)预测2016年福州市常住人口数大约为多少万人?请用所学的统计知识说明理由.

列方程 (组 解应用题:
解应用题:
某班去看演出, 甲种票每张 24 元, 乙种票每张 18 元 . 如果 35 名学生购票恰好用去 750 元, 甲乙两种票各买了多少张?