(每题4分,本题满分12分)(1)先化简,再求值
5(3a2b-ab2)-4(-ab2+3a2b),其中a=-1,b=2.
(2)某同学在计算多项式M加上x2-3x+7时,因误认为是加上x2+3x+7,结果得到答案是15x2+2x-4.试问:(1)M是怎样的整式?(2)这个问题的正确结果应是多少?
(3)“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
①用含有x、y的代数式表示右图中“囧”的面积;
②当x=4,y= 时,求此时“囧”的面积
时,求此时“囧”的面积
(·杭州市 第20题 10分)设函数y=(x−1)[(k−1)x+(k−3)](k是常数)
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象
(2)根据图象,写出你发现的一条结论
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值:
(·衢州市 第19题 6分)如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2= 图象的一个交点.
图象的一个交点.
(1)求一次函数的解析式;
(2)在y轴的右侧,当y1>y2时,直接写出x的取值范围.
(·温州卷 第19题 8分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核。甲、乙、丙各项得分如下表:
| 笔试 |
面试 |
体能 |
|
| 甲 |
83 |
79 |
90 |
| 乙 |
85 |
80 |
75 |
| 丙 |
80 |
90 |
73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分。根据规定,请你说明谁将被录用。
(·衢州市 第21题 6分)如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.
(1)求证:EG=CH;
(2)已知AF= ,求AD和AB的长.
,求AD和AB的长.
(·义乌市 第23题 12分)正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图。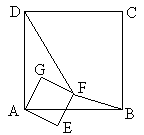
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由。