完成下面的解题过程,并在括号内填上依据。
如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数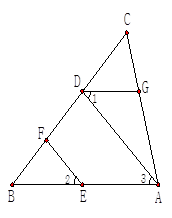 .
.
解: ∵EF∥AD,
∴∠2=____( )
又∵∠1=∠2
∴∠1=∠3
∴ ∥____( )
∴∠BAC+____=180°
∵∠BAC=85°
∴∠AGD=950
甲、乙两人分别从 、 、 这3个景点中随机选择2个景点游览.
(1)求甲选择的2个景点是 、 的概率;
(2)甲、乙两人选择的2个景点恰好相同的概率是 .
为了了解某地居民用电量的情况,随机抽取了该地200户居民六月份的用电量(单位: 进行调查,整理样本数据得到下面的频数分布表.
|
组别 |
用电量分组 |
频数 |
|
1 |
|
50 |
|
2 |
|
100 |
|
3 |
|
34 |
|
4 |
|
11 |
|
5 |
|
1 |
|
6 |
|
1 |
|
7 |
|
2 |
|
8 |
|
1 |
根据抽样调查的结果,回答下列问题:
(1)该地这200户居民六月份的用电量的中位数落在第 2 组内;
(2)估计该地1万户居民六月份的用电量低于 的大约有多少户.
已知反比例函数 的图象经过点 .
(1)求 的值.
(2)完成下面的解答.
解不等式组
解:解不等式①,得 .
根据函数 的图象,得不等式②的解集 .
把不等式①和②的解集在数轴上表示出来.

从图中可以找出两个不等式解集的公共部分,得不等式组的解集 .
如图,点 在 上,点 在 上, , ,求证: .

解方程: .