为了了解某地居民用电量的情况，随机抽取了该地200户居民六月份的用电量（单位：进行调查，整理样本数据得到下面的频数分布表．
组别 |
用电量分组 |
频数 |
1 |
50 |
|
2 |
100 |
|
3 |
34 |
|
4 |
11 |
|
5 |
1 |
|
6 |
1 |
|
7 |
2 |
|
8 |
1 |
根据抽样调查的结果，回答下列问题：
（1）该地这200户居民六月份的用电量的中位数落在第 2 组内；
（2）估计该地1万户居民六月份的用电量低于的大约有多少户．
观察下列各式及验证过程：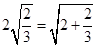
，
验证：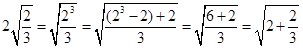
；
，
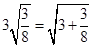验证：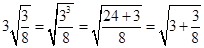
．
（1）按照上述两等式及验证过程的思路，猜想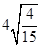
的变形结果并进行验证；
（2）针对上述各式反映的规律，写出用n（n为任意自然数，且n≥2）表示的等式，并进行证明．
一个底面为30cm×30cm的长方体玻璃容器中装满水，先将部分水倒入一个底面为正方形，高为10cm的铁桶中，当铁桶装满水时，容器中的水面下降了20cm，则铁桶的底面边长是多少？（结果保留根号）
星期天，张琪的妈妈和张琪做了一个小游戏．张琪的妈妈说：“你现在学习了二次根式，用x表示
的整数部分，用y表示它的小数部分，我这个纸包里的钱是
元，你猜一下这个纸包里的钱是多少．若猜对了，纸包里的钱就由你支配．”请你帮张琪获得这些钱的支配权．
化简下列二次根式：
(1)
；
(2)
；
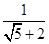(3)
(a＜0，b＞0)．
在实数范围内分解因式：
(1)x4－4；
(2)x4－4x2＋4．